 ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る*** 科目 *** 数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ高卒・大学初年度 *** 単元 *** 数と式不等式二次関数二次不等式三角比三角比と図形集合・命題・証明順列・組合せ確率整数の性質 ※高校数学Ａの場合の数・順列・組合せについて，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です． ↓積の法則 ↓和の法則 ↓場合の数のまとめ方 ↓樹形図,辞書式配列  ↓階乗 ↓階乗・順列 ↓隣り合う.合わない並び方 ↓両端指定・整数の順列 ↓円順列・じゅず順列 ↓重複順列 ↓組合せ ↓組合せ(2) ↓組合せ（文章題） ↓組分け ↓同じものがあるときの順列 ↓順路の問題 ↓番号札のもらい方 ↓二項定理，多項定理 ↓重複組合せ ↓重複組合せ（文章題） 順列，組合せ（章末問題） |
|
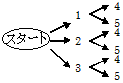
■樹形図、辞書式配列 場合の数を「もれなく」「重複なく」数えるために広く使われる方法として、「樹形図」と「辞書式配列」があります。 樹形図は、図１のように時間の経過にそって考えていくのに適しています。 辞書式配列は、図２のように出来上がったものを整理するのに適しています。
【例1】
（解答）ある試合ではA、Bの2つのチームのうち先に4勝したチームを優勝とします。 今までにAチームが3勝、Bチームが1勝しているとき、今後優勝が決まるまでの勝敗の決まり方は何通りありますか。 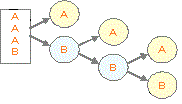 図２
（図２のように辞書式配列で考えることもできます。樹形図、辞書式配列のどちらでも自分の考えやすい方でよい。）
AAAB|A (Aが4勝になったので終わり)
AAAB|BA (Aが4勝になったので終わり) AAAB|BBA (Aが4勝になったので終わり) AAAB|BBB (Bが4勝になったので終わり) |
||||||||||||||||||||||||||||||
|
【例2】
（解答）図３において、P地点からQ地点を通ってR地点に行く行き方は何通りありますか。 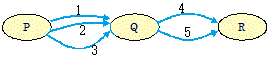 図４または図５のように考えます。6通り･･･（答）
|
||||||||||||||||||||||||||||||
|
【例3】
（解答）A、B、Cの3人が1回だけジャンケンをするとき、3人の手の出し方のうちでアイコになる出し方は何通りありますか。（アイコとは1人の勝者も1人の敗者もいないことをいいます。） 図６のように、3人とも異なる手を出す場合が6通り、3人とも同じ手を出す場合が3通りあるから 9通り･･･（答）
※ ぐー（石）を「ぐ」で、ちょき（はさみ）を「ち」で、ぱー（紙）を「ぱ」で略すものとします。 |
|
選択肢をクリックすれば採点結果と解説が出ます．暗算では無理ですから計算用紙で計算してから答えてください．
問題１x+y+z=5となる正の整数解の組は何通りありますか．
解説 xの小さい順，かつ，yの小さい順，かつ，zの小さい順の辞書式配列で考えると
x−−y−−z
の6通り
1−−1−−3 1−−2−−2 1−−3−−1 2−−1−−2 2−−2−−1 3−−1−−1 （この問題については，後に登場する重複組み合わせの問題として3H2=3+2−1C2=6という短縮答案が可能です．） |
|||
|
問題２4x+2y+z=11となる正の整数解の組は何通りありますか．
解説 xの小さい順，かつ，yの小さい順，かつ，zの小さい順の辞書式配列で考えると (1) x=1のとき，2y+z=7 1) y=1のとき，z=5 2) y=2のとき，z=3 3) y=3のとき，z=1 *) y≧4のとき，z<0になり，解なし (2) x=2のとき，2y+z=3 1) y=1のとき，z=1 2) y≧2のとき，z<0になり，解なし (*) x≧3のとき，2y+z<0になり，解なし 以上により4通り |
|||
|
問題３全く同質で区別できない白玉８個を３組に分ける方法は何通りありますか．ただし，どの組にも少なくとも１個は配り，組は区別しないものとします．
解説 組を区別しないときは，例えば１個，１個，６個と分けることと１個，６個，１個と分けることは同じことだと考えます．このような組を重複しないように数えるには，例えば個数の少ないものから順に並べて，これらを並べ替えたものは新たに数えないことにすればよい．
1,1,6 …(1)
の５通り1,2,5 …(2) 1,3,4 …(3) 2,2,4 …(4) 2,3,3 …(5) 参考：この問題と組に区別があるとき（おのおのもらう人が異なるときなど）との関係は簡単な倍率にはなりません．(1)(4)(5)は３倍，(2)(3)は６倍になり，組に区別があれば２１通りになります． |
|||
|
問題４赤玉３個，白玉２個，青玉１個の計６個の玉から３個選んで１列に並べる方法は何通りありますか．ただし，同じ色の玉は区別できないものとします．
解説 赤，白，青の順に辞書式配列で並べると
参考：この問題を後に習う「同じものがあるときの順列=組合せ」の問題として直接解くことはできません．同じものがあるときの順列の公式は全部使う場合しか適用できないので，これを適用するには，赤赤赤の組なら1通り，赤赤白の組なら３通り，...のように３個の組合せを決めてから並べ方を数えなければなりません． |
|||
|
問題５m, nが１桁の正の整数であるとき，m<nとなる組は何通りありますか．
解説 mの値の小さいもの順，nの値の小さいもの順の辞書式配列に並べると m=1のときn=2,3,...,9の８通り m=2のときn=3,4,...,9の７通り m=3のときn=4,5,...,9の６通り …… m=8のときn=9の１通り 以上から，8+7+6+5+4+3+2+1=36通り |
|||
|
問題６A，Bの２つのチームのうち先に３勝したチームを優勝とするとき，５回目の試合で優勝チームが決まるまでの勝敗の途中経過は何通りありますか．ただし，どの試合も引き分けはないものとします．
解説 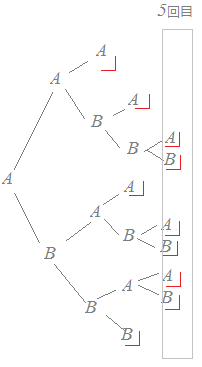 樹形図で考える．Aが初戦に勝つ場合，図のように６通りある．Bが初戦に勝つ場合も同じだけあるから，12通り． ※この問題については，後に習う「同じものがあるときの順列」=「組合せ」の考え方でも解くことができます． ５回目の試合で優勝が決まるのは，４回目の試合が終わったときに２勝２敗になっているときに限ります．このような試合経過はAABBのようにAが２個，Bが２個あるときにこれらを並べる方法の数だから，4!/(2!2!)=6通り． ５回目にどちらが勝つかで×2通り． したがって，12通りになります．  |
|
...（携帯版）メニューに戻る...メニューに戻る |
|
■［個別の頁からの質問に対する回答］[樹形図、辞書式配列について／17.5.16］
見やすい！
わかりやすい!
＝＞［作者］：連絡ありがとう． |
| ■このサイト内のGoogle検索■ |
