|
線分ABをm:nに外分する点Qとは,
AQ:QB=m:n となるような点QをABの外側にとったもの。(下図参照)  |
|
≪要点1≫
2点A,Bを結ぶ線分ABをm:nに外分する点Qの位置ベクトルは 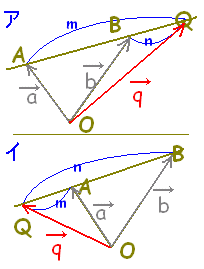
■[解説]
m>n のとき,図アにより m<n のとき,図イにより AQ:QB=m:n だからAQ:AB=m:(n-m) AQ,ABは逆向きだから 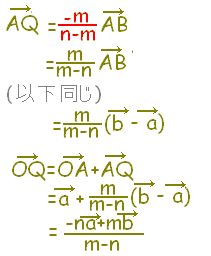 |
|
線分ABをm:nに外分する点Qとは,
AQ:QB=m:n となるような点QをABの外側にとったもの。(下図参照)  |
|
≪要点1≫
2点A,Bを結ぶ線分ABをm:nに外分する点Qの位置ベクトルは 
■[解説]
m>n のとき,図アにより m<n のとき,図イにより AQ:QB=m:n だからAQ:AB=m:(n-m) AQ,ABは逆向きだから 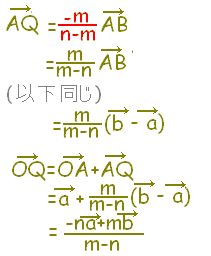 |
|
≪要点2≫
△ABCの頂点A,B,Cの位置ベクトルを各々 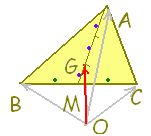
■[解説]
BCの中点Mの位置ベクトルは 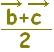 次に,A(
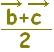 ) を2:1に内分する点がGだから, ) を2:1に内分する点がGだから,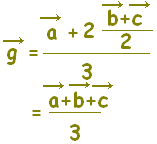 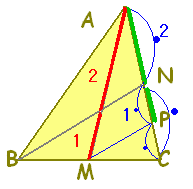 れるが,「中線の交点を求める」ためには,直線のベクトル方程式を学ぶ必要がある。 れるが,「中線の交点を求める」ためには,直線のベクトル方程式を学ぶ必要がある。ここでは、三角形の重心の定義ではなく,定義から導かれる一つの性質:「重心は頂点と対辺を2:1に内分する」を用いて,重心を求める。 MからBNに平行線を引き,ACとの交点をPとすると, PN:NA=1:2だから, AG:GM=2:1 |
|
|