※(その他,次のような不等式も証明できます)
【例4】
a, b>0のとき (2a+)(b+)≧ 9
この不等式の証明を次のように行うと間違いになります.
2a, >0だから\(2a+\dfrac{1}{b}\geqq 2\sqrt{2a\cdot\dfrac{1}{b}}\gt 0 \)…(1)
b, >0だから\(b+\dfrac{2}{a}\geqq 2\sqrt{b\cdot\dfrac{2}{a}}\gt 0 \)…(2)
辺々掛けて
\(\Bigl(2a+\dfrac{1}{b}\Bigr)\Bigl(b+\dfrac{2}{a}\Bigr)\geqq \Bigl(2\sqrt{2a\cdot\dfrac{1}{b}}\Bigr)\Bigl(2\sqrt{b\cdot\dfrac{2}{a}}\Bigr)=8 \)
…(3)
※元の不等式が≧ 9であることの証明を求めているのに対して,より「弱い」≧ 8を示しても証明にはなりません.
そもそも,○≧□>0と●≧■>0から○●≧□■となるのは,2つの不等式で「両方との等号が成り立つ場合」ですが,上の答案において
2a=となるのは 2ab=1の場合で
b=となるのは ab=2の場合なので
等号が2つとも成り立つことはありません.(1)も(2)の仮定して(3)を導くと元の条件よりも弱い条件になっています.だから,≧ 8というのは,述べていること自体は間違ってはいませんが≧ 9の証明にはなっていないのです.
(2a+)(b+)=2ab+4+1+=2(ab+)+5
ここで,a, b>0のときab, >0だから,相加平均と相乗平均の関係から
2(ab+)+5≧2(2)+5=4+5=9
等号はab=1のとき
|
|
【例5】
a, b, c>0のときbc(b+c)+ca(c+a)+ab(a+b)≧6abc
高校生が答案を書くときに「黙って使ってよい」のは「教科書に載っている公式」です.教科書に載っていない公式は,仮にあなたが知っていても黙って使うのは問題があります.
相加平均と相乗平均の関係で教科書に載っているのは2文字の場合までです.(3文字の場合はよく登場するのでギリギリセーフという解釈もできますが,4文字以上の場合はその公式を示す必要があります.)
(答案)
a, b, c, d, e, f>0のとき,相加平均と相乗平均の関係として次の不等式が成り立つ.
a+b+c+d+e+f≧6
a, b, c>0のときb2c, bc2, c2a, ca2, a2b, ab2>0だから,相加平均と相乗平均の関係により
bc(b+c)+ca(c+a)+ab(a+b)
=b2c+bc2+c2a+ca2+a2b+ab2
≧ 6
=6=6abc
等号が成り立つのは,b2c=bc2=c2a=ca2=a2b=ab2のとき
すなわちa=b=cのとき
(例えば最初の等式からb2c=bc2⇒bc(b−c)=0, b, c>0⇒b=c,以下同様にしてa=b=cが導かれる.)
|
【例6】
a, b, c>0のとき (a+)(b+)(c+)≧ 8
(証明)
a, b>0のときa, >0だから,相加平均と相乗平均の関係から
a+≧2>0
同様にして,b, c>0のときb, >0だから,相加平均と相乗平均の関係から
b+≧2>0
同様にして,c, a>0のときc, >0だから,相加平均と相乗平均の関係から
c+≧2>0
辺々掛けると
(a+)(b+)(c+)≧222=8
等号が成立するのはa=, b=, c=
からab=1 …(1), bc=1 …(2), ca=1 …(3)⇒abc=1 …(4)
(1)(4),(2)(4),(3)(4)よりa=b=c=1のとき
|
(答案)
a, b, c>0のとき , , >0だから,
相加平均と相乗平均の関係により
++≧3…(1)
さらに
(a+b)+(b+c)+(c+a)≧3>0だから
2(a+b+c)≧3>0
≧…(2)
(1)(2)より
++≧
等号が成り立つのは, a+b=b+c=c+aすなわち a=b=cのとき
|

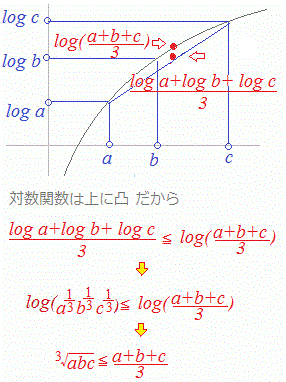
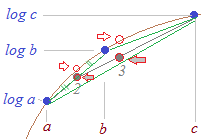 〇2点の場合
〇2点の場合