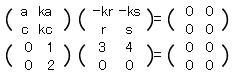零因子，可換性

■零因子

［解説］
●　数については， ａｂ＝０ならば，ａ＝0またはｂ＝０です。 (対偶で言えば，ａ≠０かつｂ≠0ならばａｂ≠０です。)

●　行列については，
ＡＢ＝０であっても，Ａ＝０またはＢ＝０　とは限りません。
(対偶で言えば，Ａ≠0かつＢ≠0でもＡＢ＝０となることがあります。)

※　教科書では，「Ａ≠0かつＢ≠0でＡＢ＝０となる行列Ａ，Ｂを零因子という」とされています。教科書としては，これ以上深入りしにくいと思いますが，授業で解説するには，逆に踏み込んだ方が(少なくともこのページの作者には)概念的に分かりやすい：
「Ａ≠0かつＢ≠0でＡＢ＝０となるときＡをＢの左零因子，ＢをＡの右零因子という。」

例
Ａ=，B=のとき，
Ａ≠0かつＢ≠0であるが， ＡＢ==

になります。
ただし， ＢＡ==

は零行列にはなりません。

●　２次以上の方程式を因数分解で解くことができるのは，左の性質によります。

ａｂ＝０ならば，ａ＝0またはｂ＝０ の性質を用いて， (ｘ－ａ)(ｘ－ｂ)＝０ ならば ｘ＝ａ　または　ｘ＝ｂ が言えます。

●　行列については零因子が存在するため，次のような変形はできません。

(Ｘ－Ａ)(Ｘ－Ｂ)＝0　→　ｘ＝ＡまたはＸ＝Ｂ
Ｘ²＝0　→　Ｘ＝0

零因子の具体例
［解説］
Ａ＝，Ｂ＝のとき，
ＡＢ＝

だから，ＡＢ＝０となるためには， ａｐ＋ｂｒ＝０・・(1)，ａｑ＋ｂｓ＝０・・(2)
ｃｐ＋ｄｒ＝０・・(3)，ｃｑ＋ｄｓ＝０・・(4) (1)はベクトル（ａ，ｂ）とベクトル（ｐ，ｒ）が垂直であればよく，
(2)はベクトル（ａ，ｂ）とベクトル（ｑ，ｓ）が垂直であればよい。
したがって，まず（ａ，ｂ）に対する関係から（ｐ，ｒ）と（ｑ，ｓ）は平行です。
次に，
(1)はベクトル（ａ，ｂ）とベクトル（ｐ，ｒ）が垂直であればよく，
(3)はベクトル（ｃ，ｄ）とベクトル（ｐ，ｒ）が垂直であればよい。
したがって，（ｐ，ｒ）に対する関係から（ａ，ｂ）と（ｃ，ｄ）は平行です。

（ａ，ｂ），（ｃ，ｄ）の傾きをｋとすると，これらは（ａ，ｋａ），（ｃ，ｋｃ）とおくことができ，これに垂直な（ｐ，ｒ），（ｑ，ｓ）の傾きは-1/ｋですが，右下図のようにｘ軸に垂直なものもありえますので，（ｐ，ｒ），（ｑ，ｓ）を（－ｋｒ，ｒ），（－ｋｓ，ｓ）とおけば，
（ａ，ｋａ）//（ｃ，ｋｃ）⊥（－ｋｒ，ｒ）//（－ｋｓ，ｓ）となります。

［問題］

１　行列の右零因子を一つ求めなさい。(文字でなく数値で答えなさい。) =	[ア]=，[イ]=，[ウ]=，[エ]= 積は
２　行列の左零因子を一つ求めなさい。(文字でなく数値で答えなさい。) =	[オ]=，[カ]=，[キ]=，[ク]= 積は
３　(少し考える問題：上の解説を参考に考えなさい。) 行列Ａ=が行列Ｂ=に対して左零因子かつ右零因子になっているような例を一つ求めなさい。(文字でなく数値で答えなさい。) (この場合，行列Ｂも行列Ａに対して，右零因子かつ左零因子となります。) = かつ =	[ケ]=，[コ]=，[サ]=，[シ]= [ス]=，[セ]=，[ソ]=，[タ]= 積は

..高卒～大学数学のメニューに戻る　 ●==メニューに戻る

■［個別の頁からの質問に対する回答］[零因子について／18.8.21］

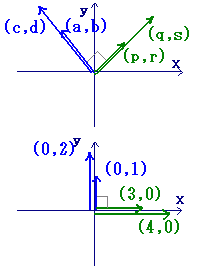
零因子の作り方のところにある文字の行列式で、(a,b)を(a,ka)とおくのは大丈夫ですが、(p,r)を(-kr,r)とおくのはなぜなんでしょうか？(a,ka)のように、y座標のとこよに、x座標に傾きをかけた値がくるのではないでしょうか？
＝＞［作者］：連絡ありがとう． $r=-\frac{1}{k}p\overset{\rightarrow}{\leftarrow}p=-kr$ だから $(r,-\frac{1}{k}p)$ とおいてもよいが，分数を避けて $(-kr,r)$ とおいても同じことになります．普通の感覚なら分数は煩わしいので，分数を避けて整数係数にします．

■［個別の頁からの質問に対する回答］[零因子について／18.8.20］

今日、零因子のところで質問したものです。ｙ軸に平行な直線は，傾きを用いたy=kxの直線の方程式によって表すことはできないということを忘れていました(というか恥ずかしながら初耳です)失礼しましたあの、零因子のところの式の例外の場合というのは、図を書いてみるのも手なんでしょうか？(というより、他に手はあるのでしょうか？)
＝＞［作者］：連絡ありがとう．「これには例外がある」ということを覚えるのです．

■［個別の頁からの質問に対する回答］[零因子について／18.8.20］

零因子の作り方のところで、昨日の質問の回答で、上の式と下の式は対応していないとのことですが、上の式は一般的な零因子の式ですよね。それが、下の具体的な零因子の式と対応してないのはおかしくないですか？
＝＞［作者］：連絡ありがとう．一般の場合と具体的な場合の関係ではありません．一般の場合と例外の場合の関係です．
高卒の方のようですが，ｙ軸に平行な直線は，傾きを用いたy=kxの直線の方程式によって表すことはできません．この話は中学，高校で何度も出て来るものです．

■［個別の頁からの質問に対する回答］[零因子について／18.8.19］

零因子の作り方のところで質問です。質問1 なぜ、(a.b) (c.d)の傾きをkとすると、これらは(a.ka)、(c.kc)とおくことができるんでしょうか？質問2 1番したの行列の左零因子で、aが0で、kaが1となっています。行列に対応？する図ではy軸上を上に向かってすすむベクトルとなってますが、このベクトルの傾きは、1/0から定義できないですよね？ですが、この場合、aが0で、kaが1となっていますから0にkをかけたら1になるということになります。でも、0になにをかけても0ですよね。ここで、この場合のkの値は何になるのでしょうか？
＝＞［作者］：連絡ありがとう．質問１について：点(a,b)が傾きkの直線y=kx上に4あるときは，b=kaが成り立つから，(a, ka)とおけます．(c,d)についても同様です．
質問2について：上の図に上の式が対応しており，下の図に下の式が対応しており，上の式と下の式は対応していません．具体的に下の式について言うと
y軸に平行なベクトル $(0,\hspace{3}1)$ とｘ軸に平行なベクトル $\begin{pmatrix}3\\ 0\end{pmatrix}$ は垂直だよね→ $(0,\hspace{3}1)\begin{pmatrix}3\\ 0\end{pmatrix}=0$
から
y軸に平行なベクトル $(0,\hspace{3}2)$ とｘ軸に平行なベクトル $\begin{pmatrix}4\\ 0\end{pmatrix}$ は垂直だよね→ $(0,\hspace{3}2)\begin{pmatrix}4\\ 0\end{pmatrix}=0$
まで，下の図に描かれた4種類の垂直を確かめているだけです．

■［個別の頁からの質問に対する回答］[零因子について／17.6.1］

採点できませんでした。
＝＞［作者］：連絡ありがとう．2000年ごろに当時全盛期だったIEでエラーが起こらないようにテストしたものですが，現存するブラウザ（Chromeも含む）では文法が合わなくなっているようですので，訂正しました．･･･このプログラム，変化の速い業界で10年以上持ちこたえたようなのでご容赦を．