○変形の基本
|
○対数をはずせる理由
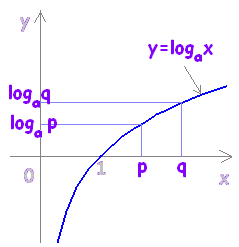
a>1のとき,y=logax のグラフは右図のように増加関数となり, 0<a<1のときは、減少関数ですが,結果は同じです。 ○底が同じ値でないとき
|
 |
○変形の基本
|
○対数をはずせる理由
a>1のとき,y=logax のグラフは右図のように増加関数となり, 0<a<1のときは、減少関数ですが,結果は同じです。 ○底が同じ値でないとき
|
 |
○変形の仕方
|
○例
log6(x-2) + log6(x-3) = log62 →log6(x-2)(x-3) = log62 →(x-2)(x-3) = 2 |
引き算のまま変形すると分数方程式になります。これを避けるには、移行して足し算にします。
○例:移行すれば
|
○真数条件と底の条件
※解を求めてから、十分条件を満たしているかどうか調べることもできますが、解が求まるとうれしくなって警戒心が薄れることが多いので、「初めに検討する」と決めておく方が安全です。
例 |
対数関数は,真数が正の数のときだけ定義されます。この真数>0 という条件(真数条件)は,元の式で検討することが重要です。変形してから真数条件を検討しても,ダメです。
例 log6(x-2) + log6(x-3) = log62 ・・(1)は log6(x-2)(x-3) = log62 ・・(2) と同じではありません。 (2)はx=1でも4でも成り立ちますが,(1)はx=1では成り立ちません。
[重要] |
○例題
log6(x-2) + log6(x-3) = log62 を解きなさい。 答案
(x-2)(x-3) = 2 x2-5x+6=2 x2-5x+4=0 x=4・・・答 |
| 例1
方程式 log2(2x-4)=log2(5-x) を解きなさい。 答案例 真数条件 ---※12x-4>0,5-x>0 より 2<x<5・・(1)方程式から ---※22x-4 = 5-x(1)(2)より |
※1 真数条件は,初めに検討する方がよいでしょう。 ※2
|
| 例2
方程式 log2(x-1) = 3 - log2(x+1) を解きなさい。 答案例 真数条件x-1>0,x+1>0 より x>1・・(1)方程式を変形してlog2(x-1)+log2(x+1) = 3 ---※1(1)(2)より |
※1
引き算は、移行して足し算にすれば、分数方程式を避けられます。 ※2
|
| 例3
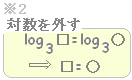
方程式 2log3x=log3(x+6) を解きなさい。 答案例 真数条件x>0,x+6>0 より x>0・・(1)方程式を変形して log3x2=log3(x+6) --- ※1x2 = x + 6 --- ※2(1)(2)よりx=3・・・答 |

 |
| 例4
方程式 答案例 真数条件 5-x>0,5x-1>0より1/5<x<5・・(1)方程式を変形して---※1(1)(2)よりx=2・・答 |
※1
|
| 例5
方程式 (log2x)2-log2x2-8=0 を解きなさい。 答案例 真数条件 x>0,x2>0よりx>0・・(1) 方程式は (log2x)2-2log2x-8=0 と書けるから log2x=Aとおくと A2-2A-8=0 (A-4)(A+2)=0 A=4,-2 log2x=4,-2よりx=16,1/4・・(2) (1)(2)よりx=16,1/4・・答 |
例6
方程式 log10x-3logx10=2 を解きなさい。 答案例 真数条件 x>0,底の条件 x>0,x≠1 よりx>0,x≠1・・(1) 底を10にそろえると方程式は
|
|
■[個別の頁からの質問に対する回答][対数方程式について/18.9.22]
logが1つだけの時の例もあったら助かります
■[個別の頁からの質問に対する回答][対数方程式について/18.2.4]
=>[作者]:連絡ありがとう.理屈の上では,ご要望のことは対数の定義のページで, 【例】 教える方からは不要と考えていましたが,学ぶ方からは必要と思う可能性がありますので,検討の余地あり.→こちら 全体的に色がありすぎて見にくい
■[個別の頁からの質問に対する回答][対数方程式について/17.11.14]
=>[作者]:連絡ありがとう.見解の相違です. 真数条件より、x>0。という表記が教科書や参考書によって書いてあったり無かったりする。全ての場合で真数は正だから、とりあえず書いておけば原点はされないだろうか。
=>[作者]:連絡ありがとう.答案全体の構成方法として,(1)原式と必要かつ十分に(つねに後戻りできるスタイルで)変形していく方法 (2)とりあえず必要条件を満たすものから捜査範囲を絞って行き,しかる後に,最後に十分性を満たさないものをはねるという方法があり得ます. (2)の方法で答案を構成する場合は,x>0は途中経過には必要とは限らず,最後に撥ねればよいことになります. あなたが,どちらのスタイルで答案を書くことが多いのか分かりませんが,初めの段階で「とりあえず書いておけば減点はされない」可能性は高いでしょう. なぜなら,満点でない答案を採点する場合(部分点を付ける場合),採点官としては横の調整上(他の採点官との公平性を確保するために),「これが書いてあれば何点」というように決めるので,その可能性は高いです. |