|
【対数方程式とは】
【例1】 log2x=8対数関数の真数や底に未知数を含む方程式を対数方程式という. → log底真数=値の形において,真数が未知数になっている 【例2】 log2(x−1)+log2(4−x)=1 → よく出る形.2つの対数で,真数が未知数になっている 【例3】 logx9=2 → log底真数=値の形において,底が未知数になっている
【対数方程式の解き方】
【例4】 log2x=3(1) 対数の定義を使って,指数の形に直す. log底真数=値 ⇔ 真数=底値 (2) 対数関数が単調増加(底>1のとき)または単調減少(0<底<1のとき)であることにより, 底が同じで「2つの対数が等しければ,真数が等しい」と言えることを利用する. log底真数1=log底真数2 ⇔ 真数1=真数2 → x=23だからx=8・・・(答) 【例5】 log2(x−1)=log2(3−x) → 両辺の底が2で同じだから,真数が等しければよい
x−1=3−x
2x=4 x=2・・・(答)
※ただし,このような問題では,式の変形をする前に「原式で真数条件を検討しておく」のがよい.
理屈の上では,得られた結果を「原式」に代入して成立することを確かめてもよいが,「答が出てしまうと,嬉しくなって,舞い上がってしまって,油断しやすくなる」ので,真数条件は初めに検討するのがお薦めです. |
【対数方程式の真数条件】
【例5】(再掲) log2(x−1)=log2(3−x)のとき(*1) (高校の数学では)対数の真数は「正の数」でなければならない. 【対数方程式の底の条件】 (*2) (高校の数学では)対数の底は「正の数」かつ「1以外」でなければならない.・・・底の条件の方が真数条件よりも厳しいことに注意
真数条件としてx−1>0, 3−x>0を満たさなければならない
【例6】 logx8=3のときしたがって,1<x<3が真数条件となる.
底の条件としてx>0, x≠1を満たさなければならない・・・(#1)
次に,x3=8よりx=2・・・(#2) (#1)(#2)よりx=2・・・(答)
《なぜ,対数方程式で,真数条件が必要なのか》
● 数学の教科書には という公式が書かれていて,これが間違ってるはずがない!と思われるかもしれませんが,「実は,この公式には,前提条件があるのです」 ● すなわち
a>0, a≠1, M>0, N>0のとき
なので,M<0, N<0などのときは,成り立つとは限らないのです.【例】 という方程式の解は,x=2だけですが という方程式の解は, すなわち,原式が(*1)のように書かれている対数方程式を(*2)のように書き換えてから解くと, (負の数)×(負の数)の形まで混ざって来ます. ● そこで,対数方程式を解くときは,「問題文を変形する前の,原式の段階で真数になっている式は,すべて正でなければならない」という真数条件を求めておくのがよい. ● 数学的には,対数方程式を解いてから,原式を満たすものだけを解としても同じことですが,「試験に臨む生徒は,問題が解けたら,嬉しくなって舞い上がってしまって,警戒心が緩みやすいのです」.だから,『緊張している最初の段階で,原式から真数条件を求めておく方が,間違いが少ない』と言えます・・・登山の事故は,全行程の4分の3を過ぎた辺りで起こる(魔の2時)といわれているのと同様です. |
 右図のように,係数を真数の指数として対数の中に取り込むとよい.
右図のように,係数を真数の指数として対数の中に取り込むとよい.
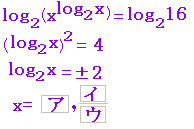 ・・(2)
・・(2)