|
■正負の数の積・商
(1) 正負の数の符号
すでに学んでいるように、正負の数には「向き」があり、正の符号+は原点から「右向き」に、負の符号−は原点から「左向き」に進むことを表しています。
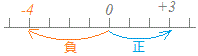 |
|
(2) 正負の数を何倍かしたもの
1) 「ある数」に ×(+2)、×(+3)、・・・というように「正の数」を掛けると、元の数の符号(原点からの向き)を変えずに大きさだけ2倍、3倍、・・・したものを表すと決めます。
例1
(+3)×(+2)=(+6)
  2) 「ある数」に ×(−2)、×(−3)、・・・というように「負の数」を掛けると、元の数の符号(原点からの向き)を逆にして大きさを2倍、3倍、・・・したものを表すと決めます。
例3
(+3)×(−2)=(−6)
  以上の例1〜4をよく見ると、符号については2種類のルール:「同じ符号の数を掛けると正の数になる」「異なる符号の数を掛けると負の数になる」とまとめられることが分かります。
同符号の2数の積は(正)
(*) 0は正の数でも負の数でもなく、0に何を掛けても0とします。また、どんな数に0を掛けても0とします。 0×(+2)=0 (−3)×0=0 |
|
(3) 正負の数を何かで割ったもの
1) 「ある数」に対して ÷(+2)、÷(+3)、・・・というように「正の数」で割ったものは、上の(2)において
,,…
のように逆数(分数)を掛けたものと同じだから、元の数の符号(原点からの向き)を変えずに大きさだけ2で割ったもの、3で割ったもの、・・・と考えることができます。2) 同様にして、「ある数」に対して ÷(−2)、÷(−3)、・・・というように「負の数」で割ったものは、上の(2)において
,,…
のように逆数(分数)を掛けたものと同じだから、元の数の符号(原点からの向き)を逆にして大きさだけ2で割ったもの、3で割ったもの、・・・と考えることができます。このようにして、割り算では「数字の大きさは、符号を取り除いたものの割り算で考えます」が、符号については掛け算と同じルール:「同じ符号の数で割ると正の数になる」「異なる符号の数で割ると負の数になる」とまとめられることが分かります。
同符号の2数の商は(正)
※(別の説明方法) 次のように考えても、割り算の符号を決めることができます。 (正)×(正)=(正) …(i) の両辺を(正)で割ると
(正)=(正)÷(正) または (正)= → (a)
(負)×(負)=(正) …(ii) の両辺を(負)で割ると
(負)=(正)÷(負) または (負)= → (b)
(正)×(負)=(負) …(iii) の両辺を(負)で割ると
(正)=(負)÷(負) または (正)= → (c)
(負)×(正)=(負) …(iv) の両辺を(正)で割ると
(負)=(負)÷(正) または (負)= → (d)
(参考)
0÷(他の数)はつねに0になりますが、(他の数)÷0という計算はできません。 0÷(+2)=0 (−3)÷0:できない 例 (+5)×(−3)=(−15) …数字は5×3=15、異符号だから符号は− ←(iii) (−7)×(−4)=(+28) …数字は7×4=28、同符号だから符号は+ ←(ii) (+18)÷(−3)=(−6) …数字は18÷3=6、異符号だから符号は− ←(c) (−10)÷(+0.5)=(−20) …数字は10÷0.5=20、異符号だから符号は− ←(d) (−24)÷(−6)=(+4) …数字は24÷6=4、同符号だから符号は+ ←(b)  |
|
◎ 以上の(2)(3)は、次のようにまとめることができます。
【要約】
|
|||||||||||||
≪問題≫ 次の図では前に書かれた数の「場所」が赤で示されています。枠の中に書かれた計算の結果を表す場所を数直線上でクリックしてください。 次の問題[第1問 / 全10問],初めの答案 [正解0問 | 誤答0問] q0 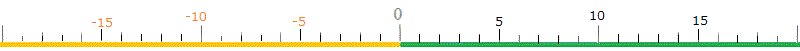

|
|
○===(携帯版)メニューに戻る ○===(PC版)メニューに戻る |