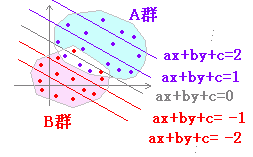
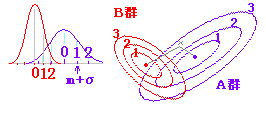
右の表1のようなデータにおいて,既知のデータの所属群A,Bを元に未知のデータの所属群A,Bを推定するのが問題であるとする.(別添ファイル hanbetu1.xls シート線形判別)
(1) 目的変数を数値に変える
所属群を表わす質的変数A,Bを各々変数1,-1に変換する.
たとえ話で言えば,右図1のようにA群の滑り台に乗れば1に,B群の滑り台に乗れば-1に行くように傾きを調整しておいて,資料を乗せてどちらに行くか調べる感じ.
(1,0でもよく,100,0でもよいが計算で出る結果がどちらの群であるか分かりやすくするには,正の数がA群を負の数がB群を表わすように平均が0となるように値を決めると分かりやすい.右の例ではAが13個Bが12個なので,12×13+(-13)×12=0とした.[平均は÷25で0])
(2) ツールの回帰分析を行う
ツール→分析ツール→回帰分析において
- 入力Y範囲を表2の水色部分
- 入力X範囲を表2の桃色部分
- ラベルにチェックを入れ
- 定数0はチェックしない
[OK] で分析結果が出力され,一番下の表左端で係数が次のようになれば
|
係数 |
| 切片 |
0.000 |
| 説明変数1 |
-2.707 |
| 説明変数2 |
5.143 |
| 説明変数3 |
8.332 |
y = 0.00 -2.707×(説明変数1) + 5.143×(説明変数2) + 8.332×(説明変数3) が重回帰式となる.
(3) 判別的中率
以上のようにして作成された重回帰式は直線的(平面的)モデルに当てはめたもので,既知のyが必ずしも所属群と一致するとは限らない.そこで右の表3のように予測値と判別結果を書き込む欄を作り,この回帰式によれば元の(既知の)データの所属群がどちらになっているか確かめる.
予測値の1つのセルにTREND()関数を書き込み
=TREND($F$2:$F$26, B$2:$D$26, B2:D2, 1)
これをコピー・貼り付けする.
判別結果の1つのセルに
=IF(G2>0,"A","B") などと値の正負によって群を判別する式を書き込みこれをコピー・貼り付けする.
※ 判別結果が正しいデータの個数/全体の個数 が判別的中率であるが,この例では判別的中率が100%になる.
(4) 未知のデータに対する所属群の予測
どちらの群に属するか分からないデータがA群に属するかB群に属するかを推定するには,右の予測値の欄で説明変数に値を入れればよい.(欄がつながっていれば予測値,判別結果が入る.もしつながっていなければ上と同様にして
=TREND(既知のY,既知のX,新しいX,1) とする.) |
表1
| No |
説明変数1 |
説明変数2 |
説明変数3 |
所属群 |
変数y |
| 標本1 |
1.947 |
2.039 |
0.452 |
A |
12 |
| 標本2 |
0.857 |
0.033 |
1.654 |
A |
12 |
| 標本3 |
0.094 |
1.062 |
1.714 |
A |
12 |
| 標本4 |
0.748 |
0.856 |
-0.450 |
B |
-13 |
| 標本5 |
1.729 |
0.033 |
-0.750 |
B |
-13 |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
| 標本25 |
-0.778 |
-1.047 |
-0.630 |
B |
-13 |
図1
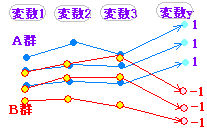 表2
表2
| No |
説明変数1 |
説明変数2 |
説明変数3 |
所属群 |
変数y |
| 標本1 |
1.947 |
2.039 |
0.452 |
A |
12 |
| 標本2 |
0.857 |
0.033 |
1.654 |
A |
12 |
| 標本3 |
0.094 |
1.062 |
1.714 |
A |
12 |
| 標本4 |
0.748 |
0.856 |
-0.450 |
B |
-13 |
| 標本5 |
1.729 |
0.033 |
-0.750 |
B |
-13 |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
| 標本25 |
-0.778 |
-1.047 |
-0.630 |
B |
-13 |
表3
| No |
説明変数1 |
説明変数2 |
説明変数3 |
所属群 |
変数y |
予測値 |
判別結果 |
| 標本1 |
1.947 |
2.039 |
0.452 |
A |
12 |
8.981 |
A |
| 標本2 |
0.857 |
0.033 |
1.654 |
A |
12 |
11.633 |
A |
| 標本3 |
0.094 |
1.062 |
1.714 |
A |
12 |
19.490 |
A |
| 標本4 |
0.748 |
0.856 |
-0.450 |
B |
-13 |
-1.368 |
B |
| 標本5 |
1.729 |
0.033 |
-0.750 |
B |
-13 |
-10.761 |
B |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
| 未知 |
1.502 |
1.403 |
1.123 |
|
|
|
|
※ 予測がうまくいかない場合でも判別的中率は50%以上にはなるので,既知のデータに対する判別的中率は低くても80%以上を目指すべきとされている.
※ 重回帰を利用しているので「変数選択」の問題にも関係するが,判別分析では判別的中率を重視する.
※ 元のデータが標準化(平均0,標準偏差1)されていれば,回帰式の係数を直接比較することにより影響力の大きな要因を見つけることができる.
ここで行った例では,説明変数3の係数が最も大きく,説明変数3が群の判別に重要な役割を果たしていることが分かる.
|