立体の表面積

→ 携帯版は別頁

== 立体の表面積(円柱，角柱，円錐，角錐の表面積) ==
［解説］
■　立体の表面積は「展開図」で考えるとよく分かります。

ア

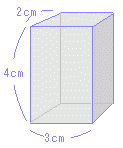
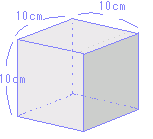右図アの立方体(正四角柱で縦横高さとも同じもの)の表面積

10×10=100(cm²)の正方形が6個あるから
600(cm²)・・・答

イ

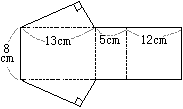
右図イの四角柱の表面積

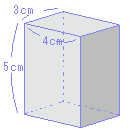
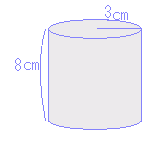
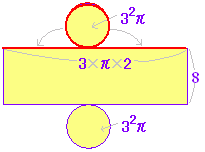
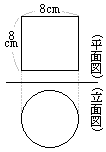
底面：3×4=12(cm²)の長方形が２つ
側面：5×4=20(cm²)の長方形が２つ
側面：5×3=15(cm²)の長方形が２つ
計94(cm²)・・・答

図ウの円柱の表面積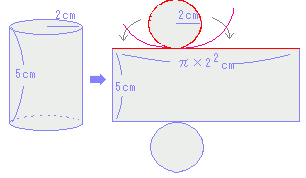ウ

底面：π×2²=4π(cm²)の円が２つ
側面：底面の円周の長さと側面の横の長さが等しいから　5×4π=20π(cm²)の長方形が１つ
計　28π(cm²)・・・答

※　数学用語の約束の問題として，
　　底面積=１つの底面の面積
　　側面積= 側面の面積の総和
だから，円柱，角柱の表面積=底面積×２+側面積　となります。
また，「底面積を求めよ」というときは，１つの底面の面積を答えます。

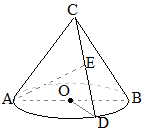
右図エの正四角錐(ピラミッド型)の表面積

エ

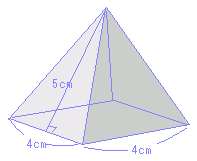
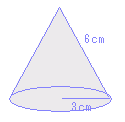
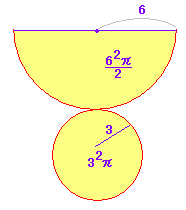
底面：4×4=16(cm²)の正方形が１つ
側面：4×5÷2=10(cm²)の三角形が４つ
計　56(cm²)・・・答

図オの円錐の表面積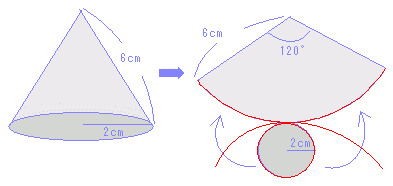
オ

まず，側面の展開図(扇形)の中心角を求めることが重要です。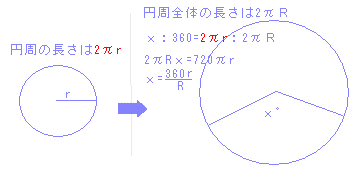
底面の円周の長さと扇形の弧(円周の一部)の長さが等しいことから，中心角をｘ°とおいてｘを求めます。

図では，ｘ=360×2÷6=120°
扇形の面積はπｒ²×中心角／360=12π(cm²)
次に，底面積はπ×2²(cm²)
計16π(cm²)・・答

採点結果：正解

，不正解

■問題■

3×4の長方形が2個→12×2=24
2×3の長方形が2個→6×2=12
2×4の長方形が2個→8×2=16
合計52(cm²)…（答）

底面積が3²π，上下2つあるから18π
底面の円周の長さが3×2×π=6πだから側面積は6π×8=48π
合計66π…（答）

底面の半径が3cmだから，底面積は3²π=9π…(1)
次に，底面の周と側面のおうぎ形の弧の長さが等しいことから，扇形の中心角Aを求める
3×2×π=6×2×π× $\frac{A}{360^{\circ}}$
$A=180^{\circ}$
側面積は
$6^2\pi\times\frac{180}{360}=18\pi$ …(2)
(1)(2)より27π…(答)

底面の半径が3cmだから円周の長さは3×2×π．これが側面の長方形の横幅になります．

側面は横幅が6π，縦が5cmの長方形だから，面積は6π×5=30π(cm²)…(答)

側面積は8×(13+5+12)=240(cm²)
底面は直角三角形で5×12÷2=30(cm²)，２個あるから60(cm²)

300(cm²)…(答)

側面は長方形で，縦の長さが8cm，横の長さは底面の円周の長さに等しい

側面の長方形の横の長さは8×πcm，縦の長さは8cmであるから，側面積は64π(cm²)…(答)

立体は円柱になり，表面積は底面積×2=16π×2(cm²)と側面積8π×7(cm²)の合計になります

底面積２つで32π(cm²)，側面積56π(cm²)の合計は88π(cm²)…(答)

※以下，８番以後の問題を解くには，中学校３年生で習う三平方の定理が必要になります．まだ習っていない場合は，三平方の定理を習ってからやってください．

底面積はS₁=4²×π=16π(cm²)
側面の扇形の中心角をθとすると

$8\pi=12\pi\times\frac{\theta}{360}$
$\theta=240^{\circ}$
側面積は $S_2=36\pi\times\frac{240}{360}=24\pi$

底面積16π(cm²)，側面積24π(cm²)の合計は40π(cm²)→2…(答)

母線の長さをL，側面の展開図における扇形の中心角をθとおくと
底面の円周と側面の扇形の弧の長さが等しいことから

$2\pi\times 2=2\pi L\times\frac{\theta}{360}$
$L\theta=720$ …(1)

表面積が40πだから

$2^2\pi+\pi L^2\times\frac{\theta}{360}=40\pi$
$L^2\theta=12960$ …(2)

(1)(2)から(2)÷(1)

$L=18,\hspace{3}\theta=40$

三平方の定理を使って高さを求めると

$h^2+ 2^2=18^2$

$h=8\sqrt{5}$ …(答)

直角三角形△ABCの面積は2×2÷2=2(cm²)
直角三角形△ABFの面積は2×4÷2=4(cm²)
直角三角形△BCFの面積は2×4÷2=4(cm²)
二等辺三角形△ABCの辺の長さは $AF=CF=\sqrt{2^2+ 4^2}=2\sqrt{5},\hspace{3}AC=2\sqrt{2}$
二等辺三角形の頂点から底辺に降ろした垂線は，底辺を二等分するから，ACの中点をMとしたとき， $AM=\sqrt{2}$
∠FMA=90°だから $AM^2+ MF^2=AF^2$
$2+ MF^2=20$
$MF=3\sqrt{2}$
三角形△BCFの面積は $3\sqrt{2}\times 2\sqrt{2}\div 2=6$ (cm²)

16(cm²) …(答)

...メニューに戻る

■［個別の頁からの質問に対する回答］[立体の表面積について／17.3.30］

問題もあり採点もできるのでその場で確認できていいと思います。このような事が増えればもっと活用できるかと思います。色なども使われていてどこか大切かわかりやすかったです。
＝＞［作者］：連絡ありがとう．

■［個別の頁からの質問に対する回答］[立体の表面積について／17.3.15］

問題もあってすごく良かったです
＝＞［作者］：連絡ありがとう．