|
○ 相似図形では3組の辺の長さの比は等しい.
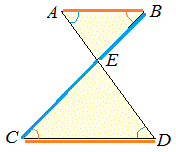 たとえば,右の図形で AB//CD のときは△ABE と△DCE は相似図形になり,BE:CE=AB:DC=AE:DE が成り立つ.
たとえば,右の図形で AB//CD のときは△ABE と△DCE は相似図形になり,BE:CE=AB:DC=AE:DE が成り立つ.だから,BE:CE の比が分かっていれば AB:DC の比が分かる. 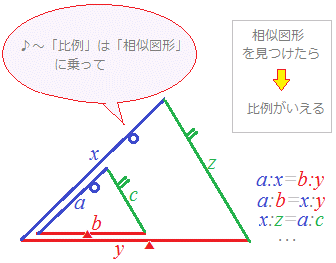 |
|
【例題1】
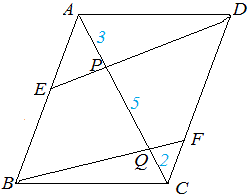
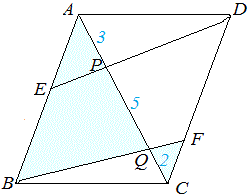
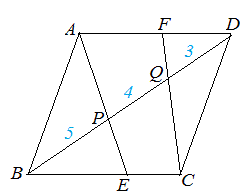
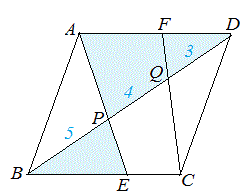
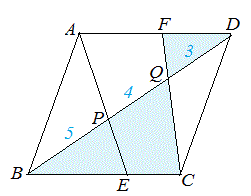
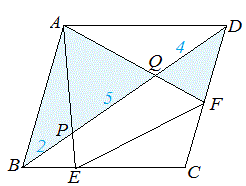
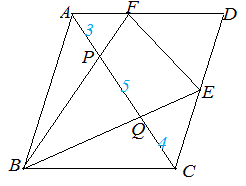
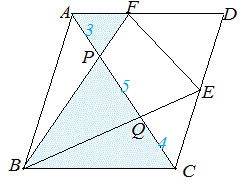
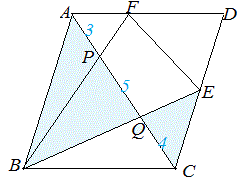
次図1の平行四辺形 ABCD において AP:PQ:QC=2:4:3 のとき, (1) AF:FD を求めなさい. 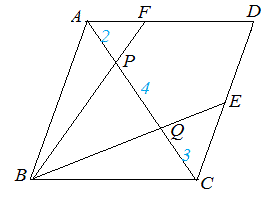 == 図1 == 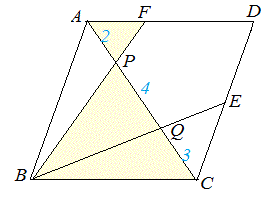 図1-1 (解答) 右図1-1のように△APF と△CPB は相似だから,AF:CB=AP:CP=2:7 四角形ABCD は平行四辺形だから AD=BC AF:AD=2:7 ゆえに AF:FD=2:(7-2)=2:5…(答)
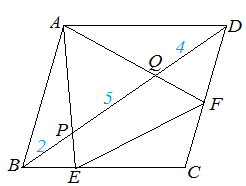
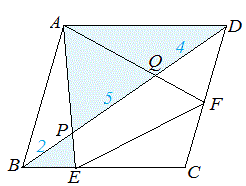
(2) CE:ED を求めなさい.
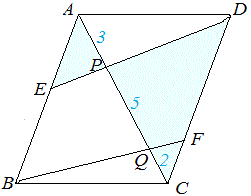
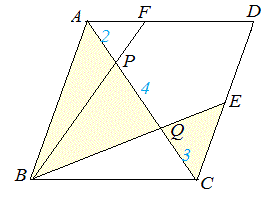 図1-2 (解答) 右図1-2のように△AQB と△CQE は相似だから,AB:CE=AQ:CQ=6:3=2:1 四角形ABCD は平行四辺形だから AB=CD CD:CE=2:1 ゆえに CE:ED=(2-1):1=1:1…(答) ⇒ このように相似図形を見つけると辺の比が求められる. |
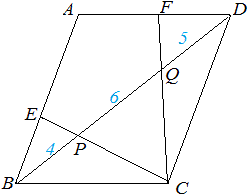
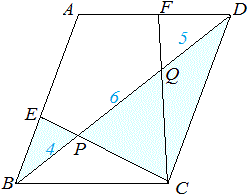 (1) △
(1) △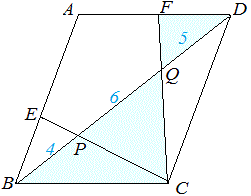 (2) △
(2) △
 (1) △
(1) △ (2) △
(2) △
 (1) △
(1) △ (2) △
(2) △
 (1) △
(1) △ (2) △
(2) △
 (1) △
(1) △ (2) △
(2) △