|
次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ. 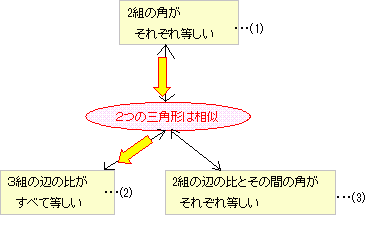 ≪図1≫ 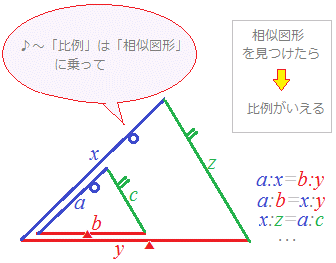 ≪図2≫
∠ABD=∠ACE
が成り立つことをいう.∠ADB=∠AEC (2)の「3組の辺の比がすべて等しい」とは,たとえば次図3では
AB:AC=BD:CE=AD:AE
が成り立つことをいう.x:y=m:n=k:l 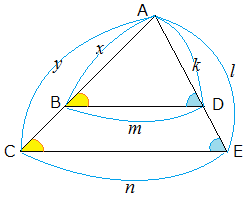 ≪図3≫ |
|
|
|
次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ.  ≪図1≫  ≪図2≫
∠ABD=∠ACE
が成り立つことをいう.∠ADB=∠AEC (2)の「3組の辺の比がすべて等しい」とは,たとえば次図3では
AB:AC=BD:CE=AD:AE
が成り立つことをいう.x:y=m:n=k:l  ≪図3≫ |
| ■平行線と線分の比 上の図3のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. BD//CE のとき ○ まず図1の(1)が成り立つ.
前に習っているから,ここでは復習になるが一応証明しておくと次のようになる.
○ 矢印に沿って考えると,△ABD∽△ACEが言える.
平行線の同位角は等しいから,
2つの角がそれぞれ等しいときは3つ目の角は180°から引いたものだから自動的に等しくなり,3つもいわなくてもよい.(実際には3つの角がそれぞれ等しくなる.)
∠ABD=∠ACE ∠ADB=∠AEC ○ さらに図1の(2)により x:y=m:n が成り立つから,これを利用すると分からない辺の長さが求められる.
◇要点1◇
上の図3において BD//CE のとき, x:y=m:n=k:l
【例】
(解答)
図3において BD//CE , x=4 , y= 6 , m=6 のとき,n の長さを求めなさい.
4:6=6:n
4n=36 n=9 …(答) |
|
【例題1】
(解答)
次図4において BD//CE , m=4 , n=5 , a=3 のとき,b の長さを求めなさい.
4:5=3:b
4b=15 b = …(答) 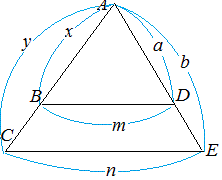 図4 14 15 16 18 2:b=3:5 → 3b=10 → b= |
|
◇要点2◇
(証明) 次図5において BF//DE となるように BF をひくと,△ABD∽△BCF,BF=DE=c となるから,
次図5において BD//CE のとき, |
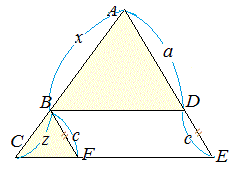 ≪図5≫ |
|
【例題2】
(解答)
次図6において BD//CE , x=12 , z=8 , a=6 のとき,c の長さを求めなさい.
12:8=6:c
12c=48 c=4 …(答) 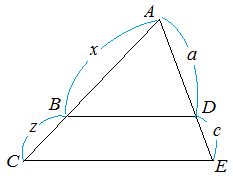 ≪図6≫ 5:2=x:3 → 2x=15 → x= |
|
【例題3】
次図7において BD//CE , m=5 , n=6 , z=2 のとき,x の長さを求めなさい. 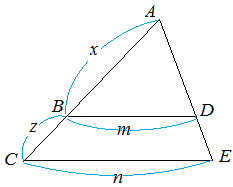 ≪図7≫ ※x:z=m:n などとはならないので注意!! 「相似図形の辺の比」にすれば等しいと言える!!
x:(x+2)=5:6
1 2 3 46x=5(x+2) 6x=5x+10 x=10 …(答) 8 18 6:(6+z)=9:12 → 9(6+z)=72 → 54+9z=72 → 9z=18 → z=2 7 8 9 10 解説 7:9=6:n 7n=54 n= …(答) |
|
2 3 4 5 解説 6 7 8 9 図8
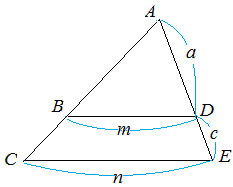 a:(a+3)=8:12
a:(a+3)=8:1212a=8(a+3) 12a=8a+24 4a=24 a=6 …(答) |
|
|