|
||||||
|
||||||
(1)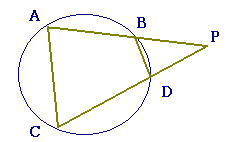 |
円外の点Pを通る2直線が円と交わる点を各々A,B及びC,Dとするとき,次のうち正しいものはどれか.(正しいものをクリック)
1 ACとBDはつねに平行になる. 2 ACとBDは決して平行にならない. 3 ACとBDは平行な場合も平行でない場合もある. 4 [ Help ] |
(2)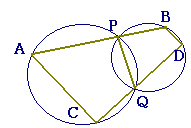 |
2円が2点P,Qで交わるとき,P,Qを通る直線が2円と交わる点を各々A,B及びC,Dとするとき,次のうち正しいものはどれか.
1 ACとBDはつねに平行になる. 2 ACとBDは決して平行にならない. 3 ACとBDは平行な場合も平行でない場合もある. 4 [ Help ] |
(3)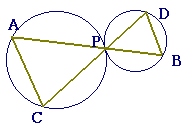 |
2つの円が点Pで外接しているとき,Pを通る2直線が円と交わる点を各々A,B及びC,Dとすると,次のうち正しいものはどれか.
1 ACとBDはつねに平行になる. 2 ACとBDは決して平行にならない. 3 ACとBDは平行な場合も平行でない場合もある. 4 [ Help ] |
(4) |
点A,B,C,Dは1つの円周上に右回りにならんでいるものとする.孤ABと孤CDの長さが等しいとき,次のうち正しいものはどれか.
1 ADとBCはつねに平行になる. 2 ADとBCは決して平行にならない. 3 ADとBCは平行な場合も平行でない場合もある. 4 [ Help ] |