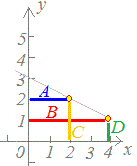|
== 関数の値と変化の割合 == ■関数の値
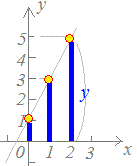
○ 関数の値(yの値)は、それぞれのxの値に応じて決まります … xの値が与えられなければ関数の値は決まりません。 ○ このyの値は右図1のように、x軸からの「縦の長さ」を表します。ただし、符号を付けて考え、x軸よりも下にあるときは負の数で表します。 例
右図1は関数y=2x+1のグラフです。このグラフにおいて、それぞれのxの値に対するyの値は、例えば次のように求めることができます。
x=0のとき、y=2×0+1=1
x=1のとき、y=2×1+1=3 x=2のとき、y=2×2+1=5 …… |
図1
 |
|
≪問題1≫ 各々正しいものを選択肢から選んでください。 |
|
|
■関数の「変化の割合」
○ 関数の「変化の割合」は、それぞれの変域に応じて決まります … 1つのxだけでは変化の割合は決まりません。
○ 関数の「変化の割合」は で定義されます。
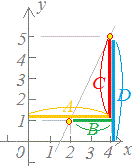
右図2においてxが1から4まで増加するときの変化の割合は に対応しています。 ○ 一次関数の「変化の割合」は、図形的には「直線の傾き」を表しています。
右図2においてxが1から4まで増加するときの変化の割合は、図形的には線分(直線を切り取ったもの)ABの傾きで示されます。
|
図2
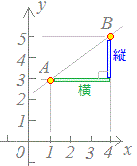 このグラフにおいてxが1から4まで増加するときの変化の割合は = |
|
≪問題2≫ 各々正しいものを選択肢から選んでください。 |
|
|
■変化の割合と途中経過
○ 上で述べたように、関数の「変化の割合」は
右図3は、A , B2人の人が500(m)の山に登ったときの時間と高さをグラフに表したものとします。で定義され、図形的には2点を結ぶ直線(線分)の傾きを表しています。 このことは、変化の割合は「初めの点」と「終りの点」だけで決まり、途中経過には関係ないということを示しています。 Aさんは初めの1時間で300(m)の高さまで登っていますが、残り3時間かけて200(m)登っているので、合計500(m)を4時間かけて登ったことになります。 Bさんは初め2時間かけて100(m)しか登っていませんが、残り2時間で400(m)登っているので、合計500(m)を4時間かけて登ったことになります。 このとき、2人とも4時間で500(m)登っているので、1時間当たりに登った高さ(高さの変化の割合)は500÷4=125(m/時)で、等しくなります。 |
図3
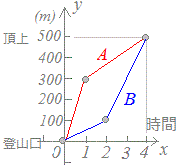 4時間かけて500(m)登っていることは同じだから、Aさんのように登っても、Bさんのように登っても、登山口から頂上までに1時間当たりに登った高さ(高さの変化の割合)は等しい。 しかし、初めから1時間後までを比較するとAさんの方が1時間当たりに登った高さ(高さの変化の割合)は大きい。 逆に、頂上の前の1時間を見るとBさんの方が1時間当たりに登った高さ(高さの変化の割合)は大きい。 |
|
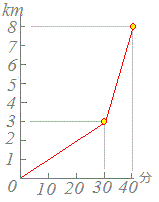
≪問題3≫ 右の図4はある人が初め30分間は徒歩で行き、残りの10分間は自転車で進んだときの、出発してからの時間と道のりの関係をグラフに表したものです。 |
図4
 |
|
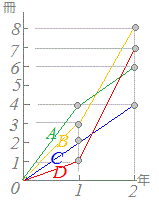
≪問題4≫ 右の図5はA , B , C , Dの4人が2年間に読んだ図書の合計を記録したものとします。この図について、各々正しいものを選択肢から選んでください。 |
図5
 |