== 変化の割合 ==
《解説》
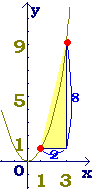
■ 次の関数 y=x2 (図1)においては,xが1から3まで変化するとき(xは2増加),yは1から9まで変化します(yは8増加). このとき,関数 y=x2の「変化の割合」は 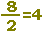 といいます. といいます.
xの増加量=xの最後の値−xの最初の値=3−1=2 です.
yの増加量=yの最後の値−yの最初の値=9−1=8 です.
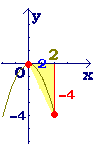
■ また,次の関数 y=−x2 (図2)においては,xが0から2まで変化するとき(xは2増加),yは0から−4まで変化します(yは4減少).このとき,関数 y=−x2の「変化の割合」は 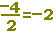 といいます.(yが減少するときの増加量はマイナスで表わします.) といいます.(yが減少するときの増加量はマイナスで表わします.)
xの増加量=xの最後の値−xの最初の値=2−0=2 です.
yの増加量=yの最後の値−yの最初の値=−4−0=−4 です.
|
|
図1
|
図2
|
■ このように,「変化の割合」は, で求めます. で求めます.
xの値でなくxの増加量,yの値でなくyの増加量で計算することになっています.
なお,yの値が途中で「増加してから減少する」ようなときも,途中経過に関係なく
yの増加量=yの最後の値−yの最初の値
と決めます. |
《問題》
左欄に書かれた変化の割合を右欄から選びなさい.
(ルール:左側から問題を一つ選択し,続けて右側からその答を選択すると消えます.間違っていれば消えません.)
|