|
《解説》
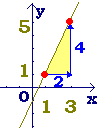
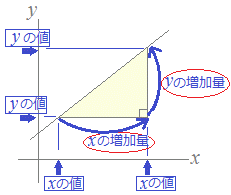
■ 次の関数y=2x−1（図１）においては，xが1から3まで変化するとき（xは2増加），yは1から5まで変化します（yは4増加）．
xの増加量
＝(xの最後の値)－(xの最初の値) ＝3−1=2です． yの増加量 ＝(yの最後の値)－(yの最初の値) ＝5−1=4です． xが1から3まで変化するとき，関数y=2x−1の 「変化の割合」は
で定義されており， 「変化の割合」は
になります．
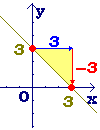
■ 他の例として，次の関数y=−x+3（図２）においては，xが0から3まで変化するとき（xは3増加），yは3から0まで変化します（yは3減少）
xの増加量
＝(xの最後の値)－(xの最初の値) ＝3−0=3です． yの増加量 ＝(yの最後の値)－(yの最初の値) ＝0−3=−3です． ｘが０から３まで変化するとき，関数y=−x+3の 「変化の割合」は
で定義されており，「変化の割合」は
になります．（※yが減少するときの増加量はマイナスで表わします．） |
【例１】
（解答）関数y=3x−4において，xの値が5から7まで増加するときの変化の割合を求めてください． 関数y=3x−4において，xの値が5から7まで増加するとき，yの値は次の表のように変化する．
yの増加量は17−11=6 変化の割合は
【例２】
（解答）関数y=−2x+1において，xの値が−2から3まで増加するときの変化の割合を求めてください． 関数y=−2x+1において，xの値が−2から3まで増加するとき，yの値は次の表のように変化する．
yの増加量は−5−5=−10 変化の割合は
|
■ このように，
|
【問題】 それぞれ正しいものを下の選択肢から選んでください．（正しいものをクリック）
(1)関数y=2x+1でxが0から3まで増加するときyの増加量を求めてください．
|
(2)関数y=−3x+5でxが1から3まで増加するときyの増加量を求めてください．
|
|
(3)関数y=3x−4でxが2から5まで増加するときの変化の割合を求めてください．
※(最後)－(最初)にすること x=5のときy=11 xの増加量は5−2=3 yの増加量は11−2=9 変化の割合は |
(4)関数y=2x+1でxが−1から3まで増加するときの変化の割合を求めてください．
※(最後)－(最初)にすること x=3のときy=7 xの増加量は(3)−(−1)=4 yの増加量は7−(−1)=8 変化の割合は |
|
【変化の割合を求めるための裏技】
【例】
♪～ただし，覚えたら一時的には楽したと思うかもしれないが，
y=ax+bのとき，変化の割合を尋ねられたら，xの係数aを答えたらよい．
長い目で見ると毒になるかもしれない～♪
▼xが「どんな値から」「どんな値まで」変化しても「変化の割合」はいつも同じ
▼定数項bの値は「変化の割合」に関係ない 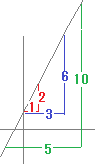 相似図形になるから， → 変化の割合は2 (2)関数y=2x+1で，xが0から3まで増加するとき → 変化の割合は2 (3)関数y=2x+1で，xが−1から4まで増加するとき → 変化の割合は2
≪式を使った解説≫
y=2x+1においてxがcからdまで増加するとき → 変化の割合は となるから，cにもdにも影響されない． さらに，定数項+1にも影響されない． |
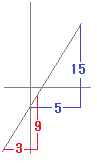 相似図形になるから， → 変化の割合は3 (5)関数y=3x−4で，xが−2から1まで増加するとき → 変化の割合は3
≪式を使った解説≫
y=3x−4においてxがcからdまで増加するとき → 変化の割合は となるから，cにもdにも影響されない． さらに，定数項−4にも影響されない． ※以上のような訳で，1次関数（直線）の変化の割合は，xの係数を見たら即答え ですが，この裏技は直線の場合しか使えないので，反比例のグラフや3年生で習う2次関数のグラフでも真似してしまうと間違います． だから，どんな問題でも対応できるようにするには，地道に 「変化の割合」は
と言えるようにした方がよい．
|
|
(5)関数y=−x+3でxが−2から1まで増加するときの変化の割合を求めてください．
※(最後)－(最初)にすること x=1のときy=2 xの増加量は(1)−(−2)=3 yの増加量は(2)−(5)=−3 変化の割合は |
(6)関数y=−3x+2でxが−4から−1まで増加するときの変化の割合を求めてください．
※(最後)－(最初)にすること x=−1のときy=5 xの増加量は(−1)−(−4)=3 yの増加量は(5)−(14)=−9 変化の割合は |
|
(7)関数y=0.2x+1.3でxが0.3から0.7まで増加するときの変化の割合を求めてください．
計算がゴチャゴチャしてきたら「裏技」でxの係数を答えるのも悪くない（ここだけ=１次関数だけの話ということを忘れないこと） x=0.7のときy=1.44 xの増加量は(0.7)−(0.3)=0.4 yの増加量は(1.44)−(1.36)=0.08 変化の割合は |
(8)関数y=−0.3x+0.4でxが−0.2から0.5まで増加するときの変化の割合を求めてください．
計算がゴチャゴチャしてきたら「裏技」でxの係数を答えるのも悪くない（ここだけ=１次関数だけの話ということを忘れないこと） x=0.5のときy=0.25 xの増加量は(0.5)−(−0.2)=0.7 yの増加量は(0.25)−(0.46)=−0.21 変化の割合は |
|
(9)関数
計算がゴチャゴチャしてきたら「裏技」でxの係数を答えるのも悪くない（ここだけ=１次関数だけの話ということを忘れないこと） xの増加量は yの増加量は 変化の割合は |
(10)関数
計算がゴチャゴチャしてきたら「裏技」でxの係数を答えるのも悪くない（ここだけ=１次関数だけの話ということを忘れないこと） x=−1のときy=−2 xの増加量は(−1)−(−4)=3 yの増加量は(−2)−(−4)=2 変化の割合は |
|
■［個別の頁からの質問に対する回答］[変化の割合について／17.4.6］
分からない
＝＞［作者］：連絡ありがとう．小学校で割合や分数が弱いと言われたことがありませんか？ |
| 髫ｨ�ｽ�ｿ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢�ｧ�ｽ�ｵ驛｢�ｧ�ｽ�､驛｢譏懶ｽｺ�･�ｽ�ｽ驍ｵ�ｺ�ｽ�ｮGoogle髫ｶﾂ隲幢ｿｽ�ｽ�ｴ�ｽ�｢髫ｨ�ｽ�ｿ�ｽ |