■直交行列とは(定義,性質)○次の4条件は互いに同値(必要かつ十分)であることを示すことができる.したがって,いずれか1つを直交行列(orthogonal matrix)の定義とすれば他は直交行列の性質となる.(*は性質としたときの記述)[前提] 直交行列は,各成分が実数である正方行列に対して定義される.
行列Pを,各成分が実数であるようなn次の正方行列とするとき,次の4条件は同値(必要かつ十分)になる.
(その他) [* 直交行列(で表される一次変換)は2つのベクトルのなす角を変えない]ことも示される.(I) tP P=P tP=E すなわち P−1=tP [* 直交行列の逆行列は転置行列に等しい]
(II) P·P=·
[* 直交行列(で表される一次変換)はベクトルの内積を変えない]
(III) |P|=||
[* 直交行列(で表される一次変換)はベクトルの大きさを変えない]
(IV) 行列Pの各列を表す列ベクトル (i=1〜n)は互いに垂直で,各々の大きさは1である.
[* 直交行列の列ベクトルは正規直交基底をなす]
○ ここでは(IV)を直交行列の定義とし,他を性質とする.
|
|
【直交行列の例】 ○ 2次の正方行列での例
(1) 各点を原点のまわりに角Θだけ回転させる行列
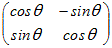
⇒ 列ベクトルの内積は cosΘ(−sinΘ+sinΘcosΘ = 0になっている.
⇒ 列ベクトルの大きさは cos2Θ+sin2Θ = 1 および (−sinΘ)2+cos2Θ = 1 になっている.
(2) 各点をx軸に関して対称に移動させる行列
○ 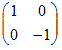 ※直交行列によって「2点の間の距離が変わらないから,すべての図形は合同な図形に移される.ただし,裏返しになることはある.」 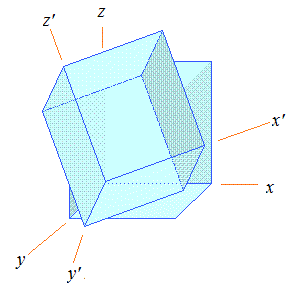 3次の正方行列での例 3次の正方行列での例
(1) 各点をx軸のまわりに角Θだけ回転させる行列
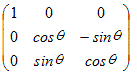 (2) 各点をy軸のまわりに角Θだけ回転させる行列 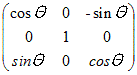 (3) 各点をz軸のまわりに角Θだけ回転させる行列 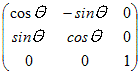
|
|||||||||||||||||||
| ■軽い確認問題 (1) 次の行列は直交行列である.この行列の逆行列を求めよ.
|
(I)により「直交行列の逆行列は転置行列に等しい」から,転置行列すなわち行と列を入れ替えたものを答えるとよい.
|
||||||||||||||||||
| (2) 直交行列Pについては各列を表す列ベクトルは互いに垂直で各々の大きさは1に等しい.このとき「各行を表す行ベクトルも互いに垂直で各々の大きさは1に等しくなる」ことを説明せよ. |
Pの転置行列も直交行列となることを示せばよい.
tP=Qとおくとき(I)により
したがって,「各行を表す行ベクトルも互いに垂直で各々の大きさは1に等しい」.
|
||||||||||||||||||
|
(3) 2つの行列P , Qが直交行列であるとき,それらの積PQも直交行列となることを証明せよ. |
(I)を用いて
t(PQ) (PQ)=(PQ) t(PQ)=Eとなることを示せばよい.
仮定により
だからt(PQ) (PQ)=(PQ) t(PQ)=Eとなる.
tP P=P tP=E …(1) tQ Q=Q tQ=E …(2) このとき t(PQ) (PQ)=tQtPPQ=tQ(tP P)Q=tQ Q=E (← (1)) (PQ) t(PQ)=PQtQ tP=P Q tQ tP=P tP=E (← (2)) |
||||||||||||||||||
|
(4) 直交行列の行列式の値は1か-1のいずれかになることを示せ. |
まず,行列の積の行列式は各々の行列式の積に等しい.
ことにより
det(AB)=det(A)·det(B)
tP P=E から det(tP) det(P)=1
次に,転置行列の行列式は元の行列の行列式に等しい.
により,det( tP)=det(P)
det( tA)=det(A)
ゆえにdet(P)2=1 よってdet(P)=±1 |
||||||||||||||||||
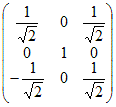
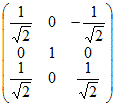
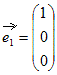 ,
,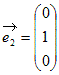 ,
,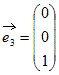 とすると,
とすると,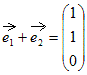
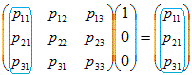 だから
だから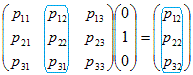 だから
だから