|
○ 行列の対角化とは
(参考)対角行列はべき乗(累乗)計算が簡単にできるなど便利な性質があり,対角行列になおすことができればメリットが大きい. 与えられた正方行列Aに対して,
P−1AP=
となるような行列Pを見つけてP−1APが対角行列になるようにすることを対角化という.
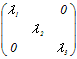
(1) 対角行列の積を求めるには対角成分を掛けるだけでよい. 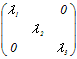 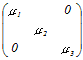 =
=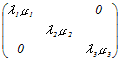
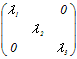 n= n=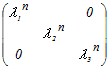
※ 「対角化せよ」という問題に対しては,
P−1AP=
の形で答えるとよい.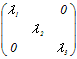
この式に左からPを,右からP−1を掛けた式,
A=P
は同じ内容を表している.
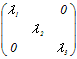 P−1 P−1
|
※注1 m×n行列とj×k行列の積はn=jの場合のみ定義される.
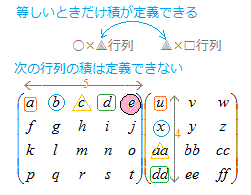 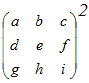 :あり , :あり ,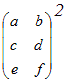 :なし :なし※注2 対角行列でない行列Aを対角行列にすることはできない.対角化とは,P−1APを対角行列にすることをいう. |
|
○ P−1APの形の式の特徴
※ 対角行列・ P−1AP= 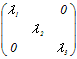 のとき のとき左辺のn乗については,
(P−1AP)n=P−1AnPが成り立つ.
右辺のn乗については
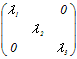 n= n=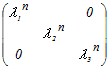 が成り立つ. が成り立つ.
P−1AnP=
両辺に左からPを,右からP−1を掛けると
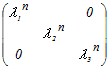
An=P
が求まる.
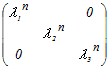 P−1 P−1
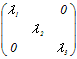 をDで表すとき,次のように変形してもよい. をDで表すとき,次のように変形してもよい.
P−1AP=D ⇒ A=PDP−1
のとき
An=( PDP−1 )n=PDnP−1=P
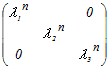 P−1 P−1
|
※ 行列の積について
(1) 交換法則は成立しない. (2) 結合法則は成立する. ある行列Pとその逆行列P−1との積は単位行列になる 結合法則を利用するとP−1APの形の式のn乗は,次のように簡単になる. ○ 2乗のとき
(P−1AP)(P−1AP)=P−1A(PP−1)AP=P−1AEAP=P−1AAP
だから
(P−1AP)2=P−1A2P
が成り立つ.○ 3乗以上のときも
(P−1AP)(P−1AP)···(P−1AP)
において隣り合うPP−1を先に計算してEにしておくと,掛け算ではすべて無視できて
=P−1APP−1AP···P−1AP
(P−1AP)n=P−1AnP
となることが分かる.
|
|
○ 対角化と累乗計算の例
例1与えられた正方行列Aに対して,
P−1AP=D (Dは対角行列)
となるような行列Pを見つける方法については,次の頁で扱う.ここでは,行列Pが見つかったときの累乗計算を示す.
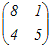 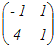 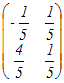 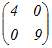 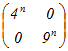 An= 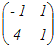 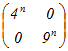 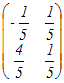 = 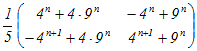
|
例2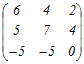 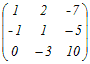 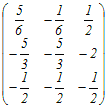 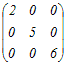 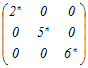 An= 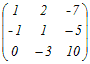 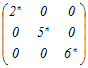 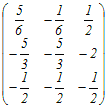
|