|
≪要点≫
 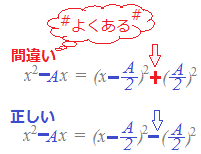
【例1】
(解答)次の2次関数の頂点の座標を求めてください. y=2x2+8x+9 x2の係数2でくくる.その際,定数項9は入れない方がよい. (←最後はかっこの外に出すので,はじめから入れない方がよい.出したり入れたりすると2度手間になり,計算間違いも多くなる.)
y=2(x2+4x)+9
かっこの中で(x+p)2の形を作る. 定数項の分は,はじめに足した分だけ引いておく.
y=2(x2+4x+4−4)+9
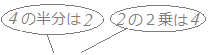 =2{(x+2)2−4}+9  外側の{ }を外す.
外側の{ }を外す.
=2(x+2)2−8+9
#よくある間違い#
先頭の係数を掛けるのを忘れてしまう!! ××2(x+2)2−4+9
=2(x+2)2+1
頂点の座標は(−2, 1)…(答)
|
【例2】
(解答)次の2次関数の頂点の座標を求めてください. y=3x2−6x+1 x2の係数3でくくる.
y=3(x2−2x)+1
かっこの中で(x−p)2の形を作る.
y=3(x2−2x+1−1)+1
=3{(x−1)2−1}+1
 外側の{ }を外す
外側の{ }を外す
=3(x−1)2−3+1
#よくある間違い#
先頭の係数を掛けるのを忘れてしまう!! ××3(x−1)2−1+1
=3(x−1)2−2
頂点の座標は(1, −2)…(答)
【例3】
次の2次関数の頂点の座標を求めてください.
(1) 3でくくったら,3で割った係数になる
(解答)(2) ⇒3を掛けた係数になる ※展開して元に戻してみると,これが正しいことが分かる 頂点の座標は (3, −3)…(答) |