|
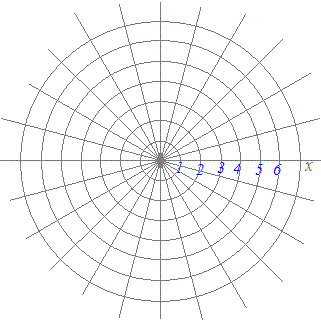
Ѓy‹ЙЌА•W‚Ж‚НЃz
Ѓ¦‹ЙЌА•W‚Ж‚µ‚Д‚Н’КЏнrЃ†0‚М‚а‚М‚р€µ‚ў‚Ь‚·‚ЄЃC•K—v‚Й‰ћ‚¶‚Дr<0‚Ж‚И‚й•\Њ»‚аЋg‚н‚к‚й‚±‚Ж‚Є‚ ‚и‚Ь‚·ЃDr<0‚М‚Ж‚«‚НЃC”јЊa‚Єђі‚Е•ОЉp‚ЄѓЖ+ѓО‚М“_‚р•\‚·‚а‚М‚Ж‚µ‚Ь‚·ЃDЃ@•Ѕ–КЏг‚М“_‚рЃCЊґ“_‚©‚з‚М‹——Јr‚ЖЋnђьЃixЋІ‚Мђі‚МЊь‚«Ѓj‚©‚з‚М•ОЉpѓЖ‚М‘g(r, ѓЖ)‚Е•\‚µ‚Ѕ‚а‚М‚р‹ЙЌА•W‚Ж‚ў‚ў‚Ь‚·ЃD 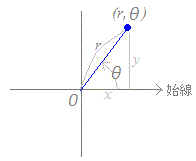 Ѓ¦’†ЉwЌZ‚ЕЏK‚Б‚Ѕ’јЊрЌА•W(x,y)‚Ж‹ЙЌА•W(r, ѓЖ)Ѓi‚Ѕ‚ѕ‚µЃCrЃ†0‚Ж‚·‚йЃDЃj‚Ж‚НЃCЋџ‚МЉЦЊW‚Є‚ ‚и‚Ь‚·ЃD Ѓm‹ЙЌА•WЃЁ’јЊрЌА•WЃn
x=r cosѓЖ
Ѓm’јЊрЌА•WЃЁ‹ЙЌА•WЃn
y=r sinѓЖ
r=
ѓЖ‚Н
cosѓЖ=
‚Ж‚И‚йЉp
sinѓЖ= |
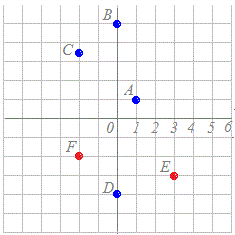 Ѓy—бЃz
Ѓy—бЃz(1) ‰Eђ}‚МA ’јЊрЌА•W‚Н(1,1) ‹ЙЌА•W‚Н(,) (2) ‰Eђ}‚МB ’јЊрЌА•W‚Н(0,5) ‹ЙЌА•W‚Н(5,) (3) ‰Eђ}‚МC ’јЊрЌА•W‚Н(−2,2) ‹ЙЌА•W‚Н(4,) (4) ‰Eђ}‚МD ’јЊрЌА•W‚Н(0,−4) ‹ЙЌА•W‚Н(4,) (*) ђ}‚М“_E ‹ЙЌА•W‚Ж‚µ‚Д(3,−)‚̂悤‚ЙѓЖ<0‚Ж‚И‚йЉp“x‚рЋg‚¤‚±‚Ж‚Є‚ ‚и‚Ь‚·ЃD Ѓ@€к”К‚ЙЃCѓЖ+2nѓОЃin‚Нђ®ђ”Ѓj‚Н‚·‚Ч‚Д“Ї‚¶•ОЉp‚р•\‚·ЃD‹ЙЌА•W(r, ѓЖ)ЃЁђ}‚М‘О‰ћ‚Н‚Ѕ‚ѕ‚P’К‚и‚Е‚·ЃD Ѓ@ђ}ЃЁ(r, ѓЖ)‚МЏкЌ‡‚НЃCr , ѓЖ‚МЋж‚и“ѕ‚й’l‚М”Н€Н‚р’и‚Я‚И‚Ї‚к‚О•K‚ё‚µ‚а‚P‚В‚ЙЊ€‚Ь‚и‚Ь‚№‚сЃD ’КЏн‚НЃCrЃ†0‚Ж‚·‚й‚М‚ЕЃCr‚Н‚Ѕ‚ѕ‚P’К‚и‚ЙЊ€‚Ь‚и‚Ь‚·ЃD ‚Ь‚ЅЃC’КЏн‚Н•ОЉp‚р0Ѓ…ѓЖ<2ѓО‚Ж‚·‚й‚М‚ЕЃCѓЖ‚Н‚Ѕ‚ѕ‚P’К‚и‚Й’и‚Ь‚и‚Ь‚·ЃD (*) ђ}‚М“_F ‹ЙЌА•W‚Ж‚µ‚Д(−2,)‚̂悤‚Йr<0‚Ж‚И‚йЏкЌ‡‚Н (2,)‚Ж“Ї‚¶‚Й‚И‚и‚Ь‚·ЃD |