|
�y�_�ƒ����̋����̌����z
�i���̌����j �����S�҂��ׂ�₷�����Ƃ���(���̂P)
�@
�����S�҂��ׂ�₷�����Ƃ���(���̂Q)�@�}������Ε�����悤�ɁC�_ �@���̌����̕��q�ɏ����Ă���̂́C�������łȂ����ł��D���m�Ɍ����u���̒l�v�ł��D �@�Ⴆ�C
�@�����̑O�̓��ɁC�����̌`���ڂ���Ɗo���������̐��k���悭���ԈႢ�́C����ɂQ�̐������������Ƃ������Ƃ���C���̂悤�ɂQ�̐����Ă͂߂�X���ł��D
�_  �@�������悭����ƁC�_�̍��W
�@�������悭����ƁC�_�̍��W |
|
�i��̗�ƃC���X�g�ɂ�����j �@�_(1, 2)�ƒ���x+y−1=0�̋������l���Ă݂܂��D 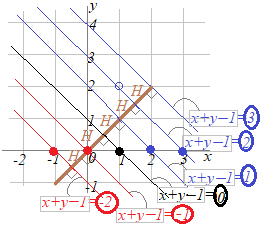
�@����x+y−2=0��̓_(2, 0)�̍��W��x+y−1�ɑ������ƁC2+0−1=1�ɂȂ�܂��D����́Cx+y−2=0 �� x+y−1=1�ƂȂ邱�Ƃ����������܂��D���̎���́C����x+y−2=0��̓_(1, 1)��(0, 2)�ɂ��Ă����l�ŁC����x+y−2=0��̓_�́C���ׂ�x+y−1�̎��̒l��1�ɂȂ�܂��D
�@����x+y−3=0��̓_(3, 0)�̍��W��x+y−1�ɑ������ƁC3+0−1=2�ɂȂ�܂��D����́Cx+y−3=0 �� x+y−1=2�ƂȂ邱�Ƃ����������܂��D
���̎���́C����x+y−3=0��̓_(2, 1)��(1, 2)�ɂ��Ă����l�ŁC����x+y−3=0��̓_�́C���ׂ�x+y−1�̎��̒l��2�ɂȂ�܂��D
�@����x+y=0��̓_(0, 0)�̍��W��x+y−1�ɑ������ƁC0+0−1=−1�ɂȂ�܂��D����́C
x+y=0 �� x+y−1=−1�ƂȂ邱�Ƃ����������܂��D���̎���́C����x+y=0��̓_(−1, 1)��(1, −1)�ɂ��Ă����l�ŁC����x+y=0��̓_�́C���ׂ�x+y−1�̎��̒l��−1�ɂȂ�܂��D
�@�ȏ�̍l�@����C����x+y−1=0�́u��ɂȂ��v�_�̍��W(x0, y0)���u���vx+y−1�ɑ�����Ă�0�ɂ͂Ȃ�Ȃ����C����x+y−1=0����̋����ɉ����āu���s���̎Ȗ͗l�ɂȂ�v���Ƃ�������܂��D�����ŁC�_(x0, y0)�ƒ���x+y−1=0�Ƃ̋��������߂�ɂ́C����畽�s���̎Ȗ͗lx+y−1=0, x+y−1=1, x+y−1=2, ... �̂P�ڐ��蓖����̊Ԋu���|����悢���ƂɂȂ�܂��D 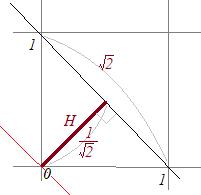 �@�E�}�ɂ����ē_(1, 0)��(0, 1)�̋����́C�P�ӂ̒������P�̐����`�̑Ίp���̒���������C
�@�E�}�ɂ����ē_(1, 0)��(0, 1)�̋����́C�P�ӂ̒������P�̐����`�̑Ίp���̒���������C�@�����ŁC���߂ɍl�������F�u�_(1, 2)�ƒ���x+y−1=0�̋����v�����߂�ɂ́C �@�܂��C�_�̍��W(1, 2)���̕������̍��ӂ������o������x+y−1�ɑ�����āu���̒l�v�����߂�D 1+2−1=2 ���ɁC���̎��̒l2�ɎȖ͗l�P�ڐ��蓖����̊Ԋu |
|
�i�����ɐ�Βl���K�v�ȗ��R�j �@�O�̐}�ɂ����āC���ʑS�̂� x+y−1=0, x+y−1=1, x+y−1=2, ...�C x+y−1=−1, x+y−1=−2, x+y−1=−3, ...�̂悤�ɁC�u���vx+y−1�́u�l�v..., −2, −1, 0, 1, 2, 3, ...�����������s���̎Ȗ͗l�ɕ������邪�C�_�ƒ����̋����́u���܂��͂O�v�̐��ōl����̂ŁC���̐�..., −3, −2, −1�ȂǂɂȂ�Ƃ���́C�������t�ɂȂ��Ă��邾���ŋ����͐��̒l3, 2, 1�ɓǂݑւ��Ȃ���Ȃ�Ȃ��D���̂悤�ɂ��āCax0+by0+c�̒l�����ɂȂ�ꍇ�͐��̐��ɒ����C���̐��̏ꍇ�͂��̂܂g���悤�ɐ�Βl��t����ƁC�ǂ�ȏꍇ�ł��g����悤�ɂȂ�D |ax0+by0+c| �i�P�ڐ���̊Ԋu�� 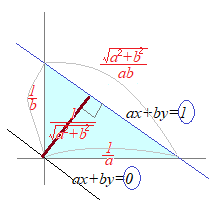 �@�E�}�̂悤�ɁCax+by�̒l��1�����Ⴄ�Ƃ��C���s�ȂQ�̒����̊Ԋu�́C���̂悤�ɋ��߂邱�Ƃ��ł���D
�@�E�}�̂悤�ɁCax+by�̒l��1�����Ⴄ�Ƃ��C���s�ȂQ�̒����̊Ԋu�́C���̂悤�ɋ��߂邱�Ƃ��ł���D�@ax+by=1 (a, b��0)�̒����ɂ��āCy=0�̂Ƃ� �@����́C�Εӂ̒��� �i�����̂܂Ƃ߁j �_(x0, y0)�ƒ���ax+by+c=0 (a2+b2��0)�̋����� |
|
�y���1.1�z
�i�j�@�_(1, 2)�ƒ���3x+4y−5=0�̋��������߂Ă��������D
�y���1.2�z
�i�j�@�_(2, 0)�ƒ���y=2x+1�̋��������߂Ă��������D �@�����̕�������2x−y+1=0�̌`�ɕό`���Ă���
�y���1.3�z
�i�j�@���_(0, 0)�ƒ���4x−3y=25�̋��������߂Ă��������D �@�����̕�������4x−3y−25=0�̌`�ɕό`���Ă���
�y���1.4�z
�i�j�@�_(4, −5)�ƒ���x=−1�̋��������߂Ă��������D �@�����̕�������x+0y+1=0�̌`�ɕό`���Ă��� |
|
�y���P�z�@�i�I�����̒����琳�������̂��P�N���b�N�j ������C������o�܂��D
(1)
�@�_(3, −4)�ƒ���2x−y−5=0�̋��������߂Ă��������D |
|
(2)
�@���_(0, 0)�ƒ���3x+4y=5�̋��������߂Ă��������D |
|
(3)
�@�_ |
|
(4)
�@�_(1, 0)�ƒ��� |
|
�i���s�ȂQ�����Ԃ̋����j
�y���2.1�z
�i�j�@���s�ȂQ����3x+4y+1=0��3x+4y+2=0�̋��������߂Ă��������D �@����3x+4y+1=0���1�_(1, −1)��3x+4y+2=0�̋��������߂�D |
|
��ʂɁC���s��2����ax+by+c=0��ax+by+d=0�̋�����
�i�ؖ��j�ƂȂ邱�Ƃ��ؖ��ł��܂��D �@����ax+by+c=0��̂P�_��(x0, y0)�Ƃ����� ax0+by0+c=0…(1) �����藧�D �@���̂Ƃ��C�_(x0, y0)�ƒ���ax+by+d=0�̋����� �����ŁC(1)�ɂ��Cax0+by0=−c��(2)�ɑ������� �@�ȏ�̂悤�ɏؖ��ł��܂����C���2.1�̂悤�Ɉ���̒�����̓_��K���Ɍ����āC�_�ƒ����̋����̌�����K�p����Ή�����̂ŁC����(*)�͊o����܂ł��Ȃ��ł��傤�D �@��ʂɁu���ȏ��ɏ�����Ă�������͖ق��Ďg���Ă��悢�v���u���ȏ��ɏ�����Ă��Ȃ�������ق��Ďg���ƌ��_����邱�Ƃ�����v�u�g��������Ώؖ����Ă���g�������悢�v�ƍl������̂ŁC(*)�͌��ʂ��o�Ă���ڂŊm�F������x�Ɏg���Ƃ悢�ł��傤�D |
|
�y���Q�z�@�i�I�����̒����琳�������̂��P�N���b�N�j ������C������o�܂��D
(1)
�@���s�ȂQ����3x−4y−2=0��3x−4y+1=0�̋��������߂Ă��������D |
|
(2)
a, b��0�̂Ƃ��C���s�ȂQ����
�����̕�������bx+ay−ab=0, bx+ay=0�ɒ����Ă���.
�@����bx+ay−ab=0���1�_(a, 0)�� ����bx+ay=0�̋��������߂�D |
|
(3)
�@�R�_A(−1, 1), B(2, −2), C(3, 3)�_�Ƃ�����ABC�̖ʐς����߂Ă��������D 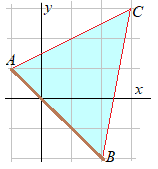 ���l�����F����AB�̒���L�����߂�D
���l�����F����AB�̒���L�����߂�D�@����AB�̕����������߂Ă���CC��AB�̋���H�����߂�D �@S=L×H÷2���ʐ� ������ �@����AB�̒����� �@����AB�̕������� x+y=0 �@�_C���璼��AB�Ɉ����������̒����� �@�ʐς� �i�ʉ�1�jBC�̒�����A����BC�܂ł̋����ŋ��߂Ă��悢�D�i�g�����͎��R�j �i�ʉ�2�j�O�p�`�̖ʐς� �i�ʉ�3�j���̒��x�̖��Ȃ�C�O���̎l�p�`�̖ʐ�4×5����C�s�v�ȎO�p�`3�̖ʐς������Ă����߂���i���w���ʼn�����j |
|
(4)
�@�R�_A(−1, 2), B(1, −3), C(2, 4)�_�Ƃ�����ABC�̖ʐς����߂Ă��������D |
|
�i���wB�̃x�N�g�����g�����ؖ��j �@���e�X�̋��ȏ��ɂ́C���w�U�ŏK���͈͂���E���Ȃ��悤�ɋC��t���Ȃ���C���ʂȂ����m�ȏؖ���������Ă��܂����C���\�����ؖ��ɂȂ��Ă���C�����̐����ό`��ڂŒǂ��Ă����̂͋�ɂ��܂��D �@���ɁC�ǂ��ɘA��čs���̂��C���ǂ��ɂ���̂��C���̕ϐ��͉���\���̂����K���������炩�łȂ��Ƃ炢�D�i���k���j �@�����ł͐��wB�̃x�N�g�����g���āC�����Ǝ��o�I�ɕ�����₷�����@�Łu�_�ƒ����̋����̌����v���ؖ����邱�Ƃ��l����D���̉����ł���ɁC�R������Ԃɂ�����u�_�ƕ��ʂ̋����̌����v���������Ƃ�ڎw���D 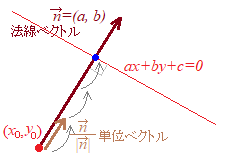 �@�����ŁC�_(x0, y0)����C���̒P�ʃx�N�g���̉��{���p�������Β���ax+by+c=0��ɂ��邩�ׂ���悢�D���̔{��t�����߂鋗���ɂȂ��D �_(x, y)���C����ax+by+c=0��ɂ��邽�߂ɂ� �@�����͐��̐������� |
|
�y�R������Ԃɂ�����_�ƕ��ʂ̋����z
�i�ؖ��j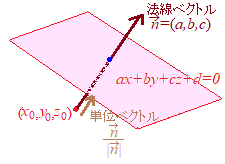 �@����ax+by+cz+d=0�̖@���x�N�g�� �@�����ŁC�_(x0, y0, z0)����C���̒P�ʃx�N�g���̉��{���p�������Ε���ax+by+cz+d=0��ɂ��邩�ׂ���悢�D���̔{��t�����߂鋗���ɂȂ��D �_(x, y, z)���C����ax+by+cz+d=0��ɂ��邽�߂ɂ� �@�����͐��̐������� |
|
�y���R�z�@�i�I�����̒����琳�������̂��P�N���b�N�j ������C������o�܂��D
(1)
�@�R������Ԃɂ����āC�_(4, 1, 2)�ƕ���2x−2y+z+4=0�̋����i�_���畽�ʂɈ����������̒����j�����߂Ă��������D |
|
(2)
�@�R������Ԃɂ����āC���_(0, 0, 0)�ƕ���2x−3y+6z+7=0�̋����i���_���畽�ʂɈ����������̒����j�����߂Ă��������D |
|
�@���ʏ�̕��s�̂Q�����̏ꍇ�Ɠ��l�ɁC�R������Ԃ̕��s�ȂQ���ʂ̊Ԃ̋����ɂ��āC���̎����ؖ����邱�Ƃ��ł��܂��D �������C�����̏ꍇ�Ɠ��l�ŁC�ۈËL���Ďg�����͈���̕��ʏ�̓_�Ƒ����̕��ʂƂ̋��������߂�����C���ĂƂ��Ă̍D���x�͏�ł��傤�D
�@���s��2����ax+by+cz+d=0��ax+by+cz+e=0�̋�����
|
|
�i�ؖ��j �@����ax+by+cz+d=0��̂P�_��(x0, y0, z0)�Ƃ����� ax0+by0+cz0+d=0…(1) �����藧�D �@���̂Ƃ��C�_(x0, y0, z0)�ƕ���ax+by+cz+e=0�̋����� �����ŁC(1)�ɂ��Cax0+by0+cz0=−d��(2)�ɑ������� |
|
�y���S�z�@�i�I�����̒����琳�������̂��P�N���b�N�j ������C������o�܂��D
(1)
�@�R������Ԃɂ����āC���s�ȂQ�̕��� |
|
(2)
�@�R������Ԃɂ����āC���s�ȂQ�̕��� |