|
【直線の方程式】
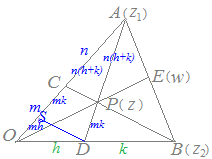
(解説)複素数平面において,点A(z1)を通り,複素数z2に平行な直線の方程式は z=z1+tz2 (tは実数) 図1のように,tを変化させると,tz2は直線の方向に伸び縮みするから,z=z1+tz2は,点A(z1)を通り,複素数z2に平行な直線上の点を指し示します.
図1
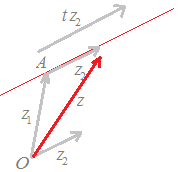
この直線の方程式において,z=z1+tz2は「直線の中に埋め込まれたもの」を表しているのではなく,原点から直線上の点に向かうものでることに注意
【2直線の交点を求めるための元になる考え方】
(解説)(複素数の1次独立) (1) z1, z2は平行でなく,0でもない複素数,p,qは実数とする. pz1+qz2=0 ならば p=q=0 が成り立つ. (2) z1, z2は平行でなく,0でもない複素数,p,q,s,tは実数とする. pz1+qz2=sz1+tz2 ならば p=s, q=t が成り立つ. 2つの複素数z1 , z2が平行であるときは,一方を他方の実数倍として表すことができます. z1=sz2 (またはz2=tz1) しかし,2つの複素数z1 , z2が平行でなく,0でもないとき, z1=sz2 (またはz2=tz1) となることはありません. (1) 平行でなく,0でもない複素数z1, z2について, pz1+qz2=0…(A) のとき,もし,p≠0ならば z1=−z2 となって,z1, z2が平行でないという仮定に反します.したがって,p=0でなければなりません. このとき, 0z1+qz2=0 qz2=0 (z2≠0) により q=0でなければなりません. 以上により,(A)が成り立つならばp=q=0でなければなりません. (2) pz1+qz2=sz1+tz2 …(B)ならば (p−s)z1+(q−t)z2=0 と変形できるから,(1)の結果からp−s=0, q−t=0でなければなりません. したがって,(B)が成り立つならばp=s, q=tになります. (係数比較が各々等しいといえるということです.) |
 【例1】
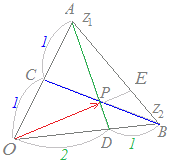
【例1】 平行線を引けば相似図形ができ,相似図形を使えば,他の辺の比を利用して辺の比を求めることができます.
平行線を引けば相似図形ができ,相似図形を使えば,他の辺の比を利用して辺の比を求めることができます.
 右図のように
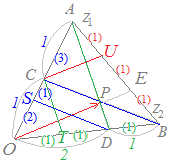
右図のように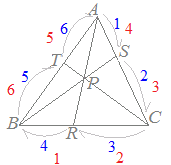 チェバの定理とは,右図のような
チェバの定理とは,右図のような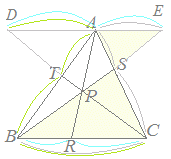 証明は,右図のように
証明は,右図のように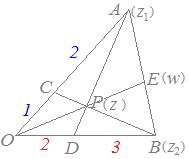 【問題1】
【問題1】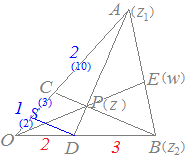
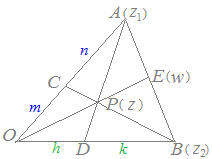 【問題2】
【問題2】