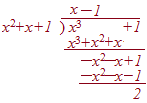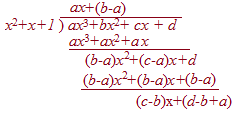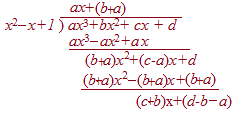|
≪剰余の定理≫
「剰余の定理」や「割り算の原理(商と余りの関係)」に関して多項式P(x)をx−αで割ったときの余りはP(α)に等しい. === よく練習するもの ===
【例1】
=== はっきりとは書いてなくても前提となっていること ===P(x)=x2+2をx−1で割ったときの余りは P(1)=12+2=3に等しい. 【例2】 P(x)=x2+2をx+2で割ったときの余りは P(−2)=(−2)2+2=6に等しい. 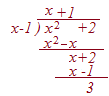 次のように「割り算」を実行すれば「商も余りも求まる」が,「剰余の定理」では割り算をしなくても「余りが求まる代わりに商は求まらない」.
次のように「割り算」を実行すれば「商も余りも求まる」が,「剰余の定理」では割り算をしなくても「余りが求まる代わりに商は求まらない」.(1) 多項式をn次式で割ったときの余りはn-1次(以下の)多項式になる. 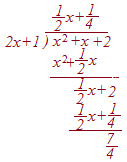 多項式の割り算では,余りが割る式と同じ次数ではまだ計算の途中とみなす.余りは必ず割る式よりも次数が低くなっていなければならない.
多項式の割り算では,余りが割る式と同じ次数ではまだ計算の途中とみなす.余りは必ず割る式よりも次数が低くなっていなければならない.だから,次の割り算のように「係数が分数になっても」余りの次数を下げなければならない. 右の例では,整数係数の多項式を整数係数の多項式で割ったときに,商も余りも有理数(分数)の係数になっている.
上記の(1)の例の通り
同様にして,「割る式,割られる式の係数の範囲」と「商と余りの係数の範囲」は次のように対応する.
(A)の整数係数の多項式割り算で商や余りが有理数になる例は上記(1)の例の通りであるが,
一般に割り算の係数の計算は和差積商の四則計算で行われるため,
整数÷整数は整数になるとは限らず,有理数になることがある.
(B)の場合,有理数は和差積商について閉じている(有理数の和差積商は有理数)であるから,有理係数多項式の割り算では商も余りも有理係数になる.しかし,四則計算では根号は登場しないから,整数係数の割り算で無理数や虚数の係数が登場することはない. (C)でも,実数は和差積商について閉じているから,実係数多項式の割り算で虚数係数の商や余りが登場することはない. →右上に続く
|
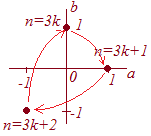
(3) 剰余の定理でαが整数でなければならないとは書いてない.一般にαは有理数でも無理数でも虚数でもよい.
【例3】
高校の教科書ではあまり登場しないが,αが無理数や虚数の場合でも使ってよい.P(x)=x2+x+2を 【例4】 P(x)=x2+x+2を 【例3】は となることを表しており 【例4】は となることを表している. したがって,これらで割ったとき,余りは等しいが商は2倍になっている.
【例題1】
(解説)整数係数の多項式f(x)をx4−4で割ると余りがx3−3になる. このときf(x)をx2−2で割ったときの余りを求めよ. 整数係数の多項式を整数係数の多項式で割っているのだから,余りは一般に有理係数多項式になる. そこでf(x)をx2−2で割ったときの余りをax+b(ただしa,bは有理数)とおける. 仮定より f(x)=(x2−2)(x2+2)S(x)+x3−3 とおけるから また f(x)=(x2−2)T(x)+ax+b(a,bは有理数) とおくと (1)(2)より a,bは有理数だから,係数を比較して a=2, b=−3 余りは2x−3…(答) ※割り算実行で行うときは次のような答案になる. f(x)=(x2−2)(x2+2)S(x)+x3−3 をx2−2で割ったとき,(x2−2)(x2+2)S(x)の部分は割り切れるから,余りはx3−3を割った部分から出てくる. 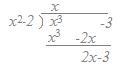 右図のように割り算を実行すれば,余りは
右図のように割り算を実行すれば,余りは2x−3…(答) (※高校生向けに平易に解説するには,この答案の方がよいでしょう.上の答案は無理数を代入しても同じ結果が得られるということの例として示した) |
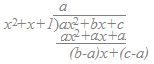 右図のように割り算を実行すれば,余りは
右図のように割り算を実行すれば,余りは