|
ゆっくり考える問題(教科書レベル)
【問題2】 (選択肢の中から正しいものをクリック)
(1)
点A(−1, 2)に関して点B(3, −4)と対称な点Pの座標を求めてください.
[未知数を (x, y)とおいて,方程式で解く方法]
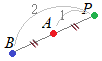
Aに関してBと対称な点がPであるとは,右図の茶色で示したように,点Aを対称の中心としてBとPが点対称であるということ.
このためには,BPの中点がAになればよい.
P(x, y)とおくと
 \( \dfrac{3+ x}{2}=-1,\hspace{10px}\dfrac{-4+ y}{2}=2 \) \( \dfrac{3+ x}{2}=-1,\hspace{10px}\dfrac{-4+ y}{2}=2 \)
を解くと
=(-5,\hspace{5}8)&chco=aa2200) \( (x,\hspace{5px}y)=(-5,\hspace{5px}8) \)…(答) \( (x,\hspace{5px}y)=(-5,\hspace{5px}8) \)…(答)
[未知数を使わずに,算数で解く方法]
Aに関してBと対称な点がPであるとは,右図の灰色で示したように,BAを2:1に外分する点がPであるということ
\times 3%2B 2\times (-1)}{2-1},\hspace{5}\frac{(-1)\times (-4)%2B 2\times 2}{2-1}\Big)=(-5,\hspace{5}8)&chco=000099) \( \small{\Big(\dfrac{(-1)\times 3+ 2\times (-1)}{2-1},\hspace{5px}\dfrac{(-1)\times (-4)+2\times 2}{2-1}\Big)=(-5,\hspace{5px}8)} \)…(答) \( \small{\Big(\dfrac{(-1)\times 3+ 2\times (-1)}{2-1},\hspace{5px}\dfrac{(-1)\times (-4)+2\times 2}{2-1}\Big)=(-5,\hspace{5px}8)} \)…(答)
|
[平行四辺形の2つの対角線は,互いに他を二等分することを使って,次の問題を解いてください]
(2)
4点A, B, C, Dをこの順にたどると平行四辺形になるという.
A(2, 2), B(−1, 1), C(0, 3)のとき,点Dの座標を求めてください.
ACの中点とBDの中点が一致すればよい
&chco=aa2200) \( D(x,\hspace{5px}y) \) \( D(x,\hspace{5px}y) \)とおくと
 \( \dfrac{2+ 0}{2}=\dfrac{x-1}{2} \) \( \dfrac{2+ 0}{2}=\dfrac{x-1}{2} \)
 \( \dfrac{2+ 3}{2}=\dfrac{y+ 1}{2} \) \( \dfrac{2+ 3}{2}=\dfrac{y+ 1}{2} \)
より
&chco=aa2200) \( D(3,\hspace{5px}4) \)…(答) \( D(3,\hspace{5px}4) \)…(答)
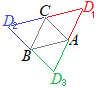
※もし,3点A,B,Cの座標が与えられていて,「平行四辺形の第4の頂点を求めよ」という問題であれば,右図のように,回り方の順序が3通り考えられるので,(1)ACの中点がBDの中点と一致する場合,(2)BCの中点がADの中点と一致する場合,(1)ABの中点がCDの中点と一致する場合の3通りの答えを書かなければならない.
|
 (解説)
(解説)
 (2)←
(2)←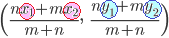

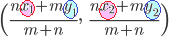 #自家受粉になっている#
#自家受粉になっている#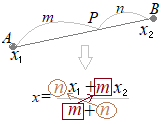 図の見かけ上は,Aの座標
図の見かけ上は,Aの座標 [未知数を
[未知数を ※もし,3点A,B,Cの座標が与えられていて,「平行四辺形の第4の頂点を求めよ」という問題であれば,右図のように,回り方の順序が3通り考えられるので,(1)ACの中点がBDの中点と一致する場合,(2)BCの中点がADの中点と一致する場合,(1)ABの中点がCDの中点と一致する場合の3通りの答えを書かなければならない.
※もし,3点A,B,Cの座標が与えられていて,「平行四辺形の第4の頂点を求めよ」という問題であれば,右図のように,回り方の順序が3通り考えられるので,(1)ACの中点がBDの中点と一致する場合,(2)BCの中点がADの中点と一致する場合,(1)ABの中点がCDの中点と一致する場合の3通りの答えを書かなければならない.