|
【内分点】 線分ABをm:nに内分する点Pとは,次の図で示した点をいいます. 【例1】 線分ABを4:3に内分する点P 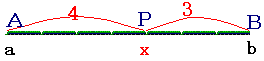 線分ABを1:2に内分する点Q 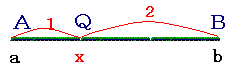 |
例1のように,内分比m:nのmがnよりも大きい場合,内分点Pは,Aから遠く,Bから近いところにあります.
例2のように,内分比m:nのnがmよりも大きい場合,内分点Qは,Bから遠く,Aから近いところにあります.
「線分ABをm:nに内分する点P」という場合,ABという文字の順序とm:nという比率の順序を対応させて考えます.すなわち,Aからの距離がmで,Bからの距離がnになる点という意味です.
したがって,例1の点Pを「線分BAを…」と書き始めた場合は,「線分BAを3:4に内分する点P」と表すことになります. 同様にして,例2の点Qは「線分BAを2:1に内分する点Q」とも書けます. |