|
【要点】
確率変数Xの期待値がm,標準偏差がσであるとき, Y=aX+b によって定められる変数Yの期待値m’,標準偏差σ’は m’=am+b…(1) σ’=|a|σ…(2) で求められる.
変数Yの分散V’は,変数Xの分散Vから次の関係で求められる.
V’=a2V…(3) Y=aX+bによって,変数Yが定義されるとき,確率分布表は次の表のようになる.
m=x1p1+x2p2+…+xnpn…(A) V=(x1−m)2p1+(x2−m)2p2+…+(xn−m)2pn σ=…(B) このとき (1)← m’=(ax1+b)p1+(ax2+b)p2+…+(axn+b)pn =a(x1p1+x2p2+…+xnpn)+b(p1+p2+...+pn) =am+b
(図1のように,個々の変数Yの定義式と同じ変換を受けます.E(Y)=aE(X)+bと書いてもよい.)
【例】
Xの期待値が2で,確率変数YがY=3X+4で定義されているとき,Yの期待値は,3×2+4=10になります. 右に続く→
|
図1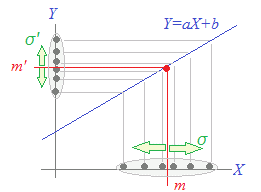 →続き (3)← Yの分散V’は, V’=(ax1+b−am−b)2p1+(ax2+b−am−b)2p2+… +(axn+b−am−b)2pn ={a(x1−m)}2p1+{a(x2−m)}2p2+…{a(xn−m)}2pn =a2(x1−m)2p1+a2(x2−m)2p2+…a2(xn−m)2pn =a2 { (x1−m)2p1+(x2−m)2p2+…(xn−m)2pn } =a2V (2)← aは正の数とは限らないので σ’==|a|=|a|σ
【例】
Xの標準偏差が5で,確率変数YがY=3X+4で定義されているとき,Yの標準偏差は,3×5=15になります. 上の図1のように,標準偏差の方は定数項4の影響を受けません.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
【例題1】
100円硬貨を2枚投げて,表がr枚出る確率は100円硬貨を投げて,表が出た金額の2倍を受け取り,使用した硬貨は参加費として取られるゲームを行う. 100円硬貨2枚を投げて,このゲームに参加するとき,差し引き儲かる金額の期待値と標準偏差を求めてください. 2Cr()r()2−r=2Cr()2 だから,表の枚数をXとすると,確率変数Xの確率分布表は次のようになる.
表がX枚のとき,儲けは100X(円)の2倍で200X(円),損失は200(円)だから,差し引き儲かる金額をYとすると, Y=200X−200 したがって E(Y)=200×E(X)−200=0(円)…(答) 次に, E(X 2)=0×+1×+4×= V(X)=E(X 2)−E(X)2= σ(X)== σ(Y)=200×σ(X)=100≒141(円)…(答)
※次のように,Y, Y 2の確率分布表を作って,直接求めることもできる.
※なお,数学の話ではないが,くじやゲームで「懸け金(参加費)の出費を伴うもの」は,宝くじや競馬のように法律で認められているものを除いて,賭博罪で罪になります.商店街や祭りのくじ引きのように「一方的にもらうだけ」のものはこれに該当しません.
E(Y 2)=40000×+0×+40000×=20000 V(Y)=E(Y 2)−E(Y)2=20000 σ(Y)==100 ここでは,Y=aX+bの定数項bを含む問題とするために,出費を伴う問題にしたもの. |
正しい番号を選択してください.
【問題1】
100円硬貨を投げて,表が出た金額の2倍を受け取り,使用した硬貨は参加費として取られるゲームを行う. 100円硬貨3枚を投げて,このゲームに参加するとき,差し引き儲かる金額の期待値と標準偏差を求めてください. (最も近いものを選んでください)
1期待値0(円),標準偏差173(円) 2期待値0(円),標準偏差200(円) 3期待値150(円),標準偏差141(円) 4期待値150(円),標準偏差200(円) HELP
100円硬貨を3枚投げて,表がr枚出る確率は
3Cr()r()3−r=3Cr()3 だから,表の枚数をXとすると,確率変数Xの確率分布表は次のようになる.
表がX枚のとき,儲けは100X(円)の2倍で200X(円),損失は300(円)だから,差し引き儲かる金額をYとすると, Y=200X−300 したがって E(Y)=200×E(X)−300=0(円)…(答) 次に, E(X 2)=0×+1×+4×+9×=3 V(X)=E(X 2)−E(X)2=3−()2= σ(X)== σ(Y)=200×σ(X)=100≒173(円)…(答) →1
|
|
【要点】
(解説)元の変数Xの平均値(期待値)がm,標準偏差がσのとき,これを偏差値Zに直すには Z=(X−m)+50…(4) ※ よく登場する偏差値と元の変数の対応関係
国語の平均点が60点で標準偏差が10点,数学の平均点が45点で標準偏差が15点というように,平均点や散らばり具合が教科・科目によって異なるときに,Aさんは国語が65点で数学が60点であったとすると,Aさんの集団の中での相対的な順位はどちらの教科が高いか?というような問題に答えるものとして「偏差値」という尺度があります. 元の変数Xの平均値(期待値)や標準偏差がどうなっていても,これを平均値(期待値)50や標準偏差10の変数に直して比較するのが偏差値です. 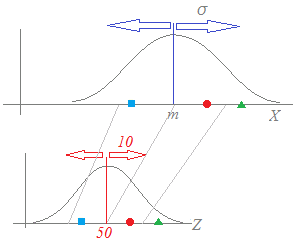 比例関係 (X−m):σ=(Z−50):10 により,偏差値Zは次の式によって求められます. Z=(X−m)+50
【例】
上の例で,Aさんの国語の偏差値は z1=(65−60)+50=55 数学の偏差値は z2=(60−45)+50=60 となるので,数学の偏差値の方が高いことになります.
※(参考)
(4)式で定義される偏差値をそのまま使う限り,偏差値が100以上になることも,負の値になることも起り得ます. △例えば,平均が30点で標準偏差が10点の試験で,ある人の得点が90点の場合は,偏差値110になります. ▼平均が55点で標準偏差が10点の試験で,ある人の得点が0点の場合は,偏差値−5になります. |
【問題2】
ある学年で英語の平均点が65点で標準偏差が8点であった.その試験でAさんの得点が75点であったとき,Aさんの英語の偏差値を求めてください. 155.0 257.5 360.0 462.5 HELP
英語の平均点が65点,標準偏差が8点のものを,平均点が50点で標準偏差が10のものに変換します.
z=(65−65)+50=62.5 →4
m=55, σ=12だから
m+σ=67 →3
|
|
【要点】
(解説)変数の基準化(規格化,標準化)とは,平均値が0,標準偏差が1となる変数に変換すること. 元の変数Xの平均値(期待値)がm,標準偏差がσのとき,基準化(規格化,標準化)した変数をZとすると Z= ←→ X=m+Zσ…(5) ※ 基準化(規格化,標準化)された変数Zと元の変数Xの対応関係
統計においては,身長と体重,国語の得点と数学の得点のように,測定の単位や平均,標準偏差の異なるデータを比較するために,各々の変数を平均値が0,標準偏差が1となる変数に変換して使うことが多い. 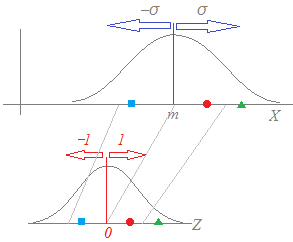 Z= ←→ X=m+Zσ
【例】
ある学級の生徒の身長について,平均が165(cm),標準偏差が8(cm)のとき,身長x1=160(cm),x2=172(cm)という2人のデータを基準化すると x1=160 → z1=−0.625 x2=172 → z2=0.875 |
Z==1.5 すなわち 21.0=15.0+1.5×4.0 だから,z1=1.5に変換されます. →3
基準化された変数Zの「平均値はつねに0」,「標準偏差はつねに1」になりますので,真ん中あたりが0になっていない2,3,4は答えになる可能性がありません.
→1
|
|
今日では,統計計算をコンピュータで行うことが多いので,次に述べる仮平均法(簡便計算法)を使わずに,直接計算することもできますが,筆算で平均値や標準偏差を求めるときは,小さな整数値で処理する仮平均法(簡便計算法)が便利です.
【仮平均法(簡便計算法)の原理】
(解説)一般に,階級幅cの度数分布表において,仮平均をx0として仮変数uを導入するとき,元の変数xを用いた計算が複雑な小数計算であっても,uを用いた計算は,階級幅1の簡単な整数値の計算でできます. このとき,E(u)からE(x)へは次の式で戻すことができます. E(x)=cE(u)+x0 σ(x)=cσ(u) 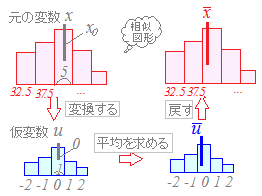
右の表のように,階級幅5 (37.5−32.5=5, 42.5−37.5=5)の度数分布表が与えられているとき,この表から平均や標準偏差を計算するためには,込み入った小数計算をしなければなりませんが,仮平均を使って変数を変換すると,簡単な1桁の整数計算でできるようになります. 度数分布表の中央付近で,度数の最も大きい階級(この表では,赤で示した42.5)の階級値を仮平均u=0として,増える方向に1, 2, ..,減る方向に−1, −2, ..という階級値を仮変数ukとして割り当てます. このように仮変数ukとして割り当てると,ukは0の近くの小さな整数値なので,掛け算,足し算などが楽にできます. E(u)=(3×(−2)+5×(−1)+0+4×1+1×2)÷20 =(−6−5+4+2)÷20=(−5)÷20=−0.25 E(x)=5×(−0.25)+42.5=41.25 E(u2)=(3×4+5×1+0+4×1+1×4)÷20 =(12+5+4+4)÷20=25÷20=1.25 V(u)=E(u2)−E(u)2=1.25−0.0625=1.1875 σ(u)==1.09 σ(x)=5×1.09=5.45
仮平均法(簡便計算法)では,「中央付近」かつ「度数が大きい階級値」を仮平均x0に選ぶのがコツ
⇒ 0を掛けることになって,計算が省略できる. |
【問題6】
元の変数Xについて,階級幅5の度数分布表に表されているとき,仮平均をx0=35.5として仮変数を使って求めたら,E(u)=0.1 , σ(u)=1.22となった.このとき,元の変数Xの平均と標準偏差は次のうちどれか. 1平均35.5,標準偏差1.22 2平均35.5,標準偏差41.6 3平均36.0,標準偏差6.1 4平均36.0,標準偏差41.6 HELP
x=cu+x0だから
E(x)=cE(u)+x0=5×0.1+35.5=0.5+35.5=36.0 σ(x)=cσ(u)=5×1.22=6.1 →2
σは,x0に無関係です
【問題7】
1E(u)=−0.1, σ(u)=1.0 2E(u)=0.0, σ(u)=1.0 3E(u)=0.1, σ(u)=1.5 4E(u)=0.2, σ(u)=1.5 HELP 1E(x)=34, σ(x)=6 2E(x)=34, σ(x)=10 3E(x)=35, σ(x)=8 4E(x)=35, σ(x)=10 HELP
E(u)=(-4-3+5+2)/20=0 E(u2)=(8+3+5+4)/20=1 だから V(u)=1-0=1 σ(u)=1 →2
E(u)=0
σ(u)=1 だから E(x)=0+35=35 σ(u)=10×1=10 →4
|