■まえがき
整数係数の方程式の作り方

例
　ｘ＝２＋√3　が１つの解となる２次方程式を作るとき，この式の両辺を２乗してしまうと
ｘ２＝４＋４√3＋３＝７＋４√3　
となって，√3が残ります．		 （参考）
ｘ２＝７＋４√3　の解は，ｘ＝−２−√3，２＋√3です．
　ｘ＝２＋√3　が１つの解となる整数係数の２次方程式は次のように作ることができます．
ｘ＝２＋√3　
(移項)→　ｘ−２＝√3
(両辺を２乗する)→ｘ２−４ｘ＋４＝３
ｘ２−４ｘ＋１＝０
 （参考）
ｘ２−４ｘ＋１＝０　の解は，ｘ＝２−√3，２＋√3です．
【要点】　　√n　だけを右辺に残して２乗する． （参考）
　x2=(m+√n)2＝ｍ２＋２ｍ√n＋ｎ　では√が残ります．

■本題
式の値（複雑な無理数の代入）

例
　「ｘ＝２＋√3　のとき，　ｘ３−２ｘ２＋３ｘ−１３　の値を求めなさい」というような問題において，ｘに　２＋√3　を直接代入すると，計算が大変で計算間違いも多くなります．
　このような問題においては，ｘ２−４ｘ＋１　が　０　となることを利用して，式を簡単にしてから（次数を下げてから）代入するのが普通です．
（答案例）
ｘ＝２＋√3　のとき，ｘ２−４ｘ＋１＝０・・・(1)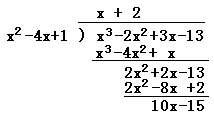
（参考）
＜１次式＞　　＜定数＝０次式＞
ｘ　のかわりに　２＋√3　を代入すると，次数が１次下がります．
＜２次式＞　　＜定数＝０次式＞
ｘ２−４ｘ＋１　に　０　を代入すると，次数を一度に下げることができます．
　なお，ｘ２＝４ｘ−１　となるので，
＜２次式＞　　＜１次式＞
ｘ２　のかわりに　４ｘ−１　を代入すると，次数は１次だけ下がります．
ｘ３−２ｘ２＋３ｘ−１３
＝（ｘ２−４ｘ＋１）（ｘ＋２）＋１０ｘ−１５・・・(2)だから
ｘ３−２ｘ２＋３ｘ−１３
＝１０ｘ−１５
＝１０（２＋√3）−１５
＝５＋１０√3・・・(答)

（よくある質問）
ｘ２−４ｘ＋１＝０　なのに，ｘ２−４ｘ＋１　で割るのは０で割ることにならないのか？

（回答）

の割り算は，ｘ２−４ｘ＋１が０以外のときに成り立ちますが
ｘ３−２ｘ２＋３ｘ−１３
＝（ｘ２−４ｘ＋１）（ｘ＋２）＋１０ｘ−１５
は，ｘ＝２＋√3　のときも含めて，すべてのｘについて成り立ちます．
　したがって，答案の本文では０を掛けていることとなり，答案にはまちがいはありません．
　なお，ｘ３−２ｘ２＋３ｘ−１３＝１０ｘ−１５
となるのはｘ＝２＋√3，２−√3のときだけで，他のｘの値に対しては，この変形は成り立ちません．

 （参考）
ｘ＝２＋√3・・・(1)
ｘ２＝４ｘ−１・・・(2)　を繰り返し適用すると，何次式でも１次または定数まで下げることができます．
ｘ３＝ｘ・ｘ２＝ｘ（４ｘ−１）
＝４ｘ２−ｘ
＝４（４ｘ−１）−ｘ＝１５ｘ−４

ｘ４＝ｘ・ｘ３＝ｘ（１５ｘ−４）
＝１５ｘ２−４ｘ
＝１５（４ｘ−１）−４ｘ
＝５６ｘ−１５

ｘ３−２ｘ２＋３ｘ−１３
＝（１５ｘ−４）−２（４ｘ−１）＋３ｘ−１３
＝１０ｘ−１５
　左の答案では，少しずつ次数を下げる代わりに，「まとめて」下げていることになります．

【要点】

　複雑な無理数を，次数の高い式に代入するには

 例
ｘ＝２＋√3　のとき，　ｘ３−２ｘ２＋３ｘ−１３　の値を求めなさい．
(1)　√ｎだけを右辺に残す．　 (1)　ｘ−２＝√3
(2)　２乗する．　 (2)　ｘ２−４ｘ＋４＝３
(3)　＝０　の形の方程式にする． (3)　ｘ２−４ｘ＋１＝０
(4)　求める式を，方程式の左辺で割る． (4)　
(5)　商と余りの関係に直す． (5)　
ｘ３−２ｘ２＋３ｘ−１３
＝（ｘ２−４ｘ＋１）（ｘ＋２）＋１０ｘ−１５
＝１０ｘ−１５　（なぜなら，ｘ２−４ｘ＋１＝０）
(6)　ｘの値は，余りに代入する．
（次数を下げてから代入するところがポイント）		 (6)　
１０ｘ−１５＝１０（２＋√3）−１５＝５＋１０√3
※　どうしても，単純に代入する方に魅力を感じる人へ：
以上に紹介した方法は，単に計算を楽にするだけのものでなく，この方法により「様々な問題に対する応用の道が開けてくる」と考えてください．

《問題》
１
　
 ｘ＝2+√5のとき，ｘ3−4ｘ2-ｘ+3の値はとなる.

2
　ｘ＝１−√5のとき，ｘ4-5ｘ2-14ｘ+3の値はとなる.

3
　のとき，ｘ３−２ｘ+３の値はとなる．
 
 

4
　ｘ＝５−√7のとき，ｘ３−８ｘ２＋ｘ＋３５の値は

　ｘ-3　ｘ+3　3ｘ-1　3ｘ+1　の値に等しい.

ヒント
　
5
　ｘ２−ｘ＝１のとき，ｘ３−２ｘの値はとなる．
 
 


←メニューに戻る