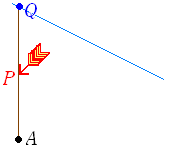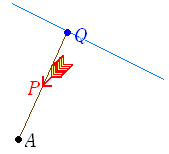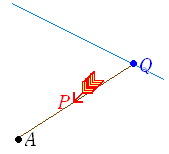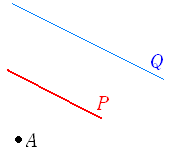
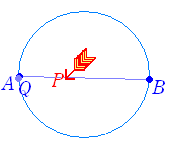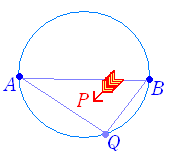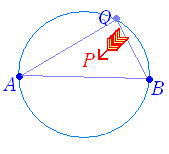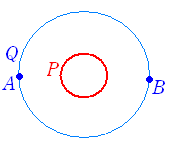
■　軌跡の方程式２

○　点が動いたあとを「軌跡」という．

例　右図１は，定点Ａと直線上を動く動点Ｑの中点Ｐの軌跡，右図2は２定点Ａ，Ｂと円周上の動点Ｑでできる三角形の重心Ｐの軌跡である．

［例題1］　［中点の軌跡］
　動点 Q が直線 x−2y+4=0 上を動くとき，定点 A(0 , 0) と点 Q の中点 P の軌跡の方程式を求めよ．
［解答］
点 Q の座標を (s , t)，点 P の座標を (x , y) とおく．
　２つの点 P , Q が動くが，軌跡の方程式を求めたいのは，点 P である．すなわち，点 P の x 座標と y 座標の「関係式」を求めれば答となる．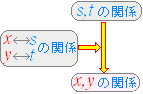
　点 Q の座標 s , t の「関係式」は与えられている．
　点 Q は直線 x−2y+4=0 上にあるから，その座標 s , t は，次の関係式を満たす．
____________s−2t+4=0 …(1)
　 P は，２点 AQ の中点だから，次の関係式が成り立つ．
____________x= …(2)

____________y= …(3)

(2)(3)より
____________s=2x , t=2y
これらを(1)に代入して s , t を消去する．
____________2x−4y+4=0 …(4)　（必要）
逆に(4)と(2)(3)から(1)が得られるから，図形(4)上の点 P に対応する点 Q は図形(1)上にある．（十分）
ゆえに，求める軌跡の方程式は x−2y+2=0 …（答）
　（参考）Ｑが描く図形とＰが描く図形は，定点を相似の中心とする相似図形になる．
［例題2］　［中点の軌跡］
　動点 Q が円 x2+(y−2)2=4 上を動くとき，定点 A(4 , 0) と点 Q の中点 P の軌跡の方程式を求めよ．
［解答］
点 Q の座標を (s , t)，点 P の座標を (x , y) とおく．
　点 Q は円 x2+(y−2)2=4 上にあるから，その座標 s , t は，次の関係式を満たす．
____________s2+(t−2)2=4 …(1)
　 P は，２点 AQ の中点だから，次の関係式が成り立つ．
____________x= …(2)

____________y= …(3)

(2)(3)より
____________s=2x−4 , t=2y
これらを(1)に代入して s , t を消去する．
____________(2x−4)2+(2y−2)2=4 …(4)
　一般に (x−a)2+(y−b)2=r2 は円を表わす．
この形に直すためには
_____(2x−4)(2x−4)+(2y−2)(2y−2)=4
の両辺を2で割っただけでは
_____(x−2)(2x−4)+(y−1)(2y−2)2=2
になり変形不十分
さらに２で割ると
_____(x−2)(x−2)+(y−1)(y−1)=1 になる．
要するに，(4)を 4 で割ればよい．
(4)の両辺を 4 で割ると
____________(x−2)2+(y−1)2=1 …(5)　（必要）
逆に(5)と(2)(3)から(1)が得られるから，図形(5)上の点 P に対応する点 Q は図形(1)上にある．（十分）
ゆえに，求める軌跡の方程式は (x−2)2+(y−1)2=1 …（答） 		図１
図２

[公式] 【内分点の公式】
　２点 A(x1 , y1 ) , B(x2 , y2 ) を結ぶ線分 AB を m : n に内分する点の座標は
( , )

【要点】　軌跡の方程式の求め方
(I)　動点の座標を (x , y ) とおく．
「軌跡の方程式」とは，「動点の x 座標と y が満たす関係式」のことと考えればよい．これを求めるためには，必ず x 座標と y 座標がいる．
　軌跡の方程式を求めるためには，動点を P(x , y ) とおくことから始める．
(II) 与えられた条件を満たす x , y の関係式を作る．
「与えられた条件　⇒　関係式（図形）」で求まる式（図形）は，与えられた条件が成立するための「必要条件」になっている．
　すなわち，「ＡならばＢ」「Ａを変形したらＢになる」とき，「Ａのときは必ずＢになる」「Ａが成り立つときは必ずＢでなければならず，これ以外にはない」という関係にある．
　しかし，このようにして得られた関係式（図形）の全部が元の与えられた条件を満たすとは限らない（元よりも広い範囲になっていることがある）ので，その内のどの部分が与えられた条件を満たすか確かめなければならない．このために，次の(III)の手順で確かめる．
　得られた関係式のうちで元の与えられた条件を満たさない点は「除外点」と呼ばれる．(III)は「除外点」の検討になっている．
(III) (II)で求めた関係式を満たす点が元の条件を満たすかどうか確かめる．
「関係式　⇒　与えられた条件」が成り立つかどうか調べる．「ＢならばＡ」が成り立つときＢはＡの「十分条件」と呼ばれる．十分条件が成り立つことを，十分性を満たすともいう．
［例題3］　［重心の軌跡］
　動点 Q が円 x2+y2=9 上を動くとき，２定点 A(−3 , 0) , B(3 , 0) と点 Q とで作られる△ABQ の重心 P の軌跡を求めよ．
［解答］
点 Q の座標を (s , t)，点 P の座標を (x , y) とおく．
　点 Q は円 x2+y2=9 上にあるから，その座標 s , t は，次の関係式を満たす．
____________s2+t2=9 …(1)
　 P は，△ABQ の重心だから，次の関係式が成り立つ．
____________x= …(2)

____________y= …(3)

(2)(3)より
____________s=3x , t=3y
これらを(1)に代入して s , t を消去する．
____________(3x)2+(3y)2=9 …(4)
(4)の両辺を 9 で割ると
____________x2+y2=1 …(5)
ただし，３点 A , B , Q が同一直線上に並ぶときは△ABQ ができないから，(5)のうち (−1 , 0) , (1 , 0) を除く．
ゆえに，求める軌跡は x2+y2=1 のうち (−1 , 0) , (1 , 0) を除いたものである． …（答）
［問題1］
　動点 Q が直線 y=2x+1 上を動くとき，定点 A(0 ,−2) と点 Q を結ぶ線分 AQ を 1 : 2 に内分する点の軌跡を求めよ．
y=x−

採点する やり直す ヘルプ
［問題2］
　動点 Q が円 (x−4)2+(y−2)2=4 上を動くとき，定点 A(2 , 0) と点 Q の中点 P の軌跡の方程式を求めよ．
中心の座標が ( , ) ，半径 の円

採点する やり直す ヘルプ
［問題3］
　動点 Q が円 (x−3)2+y2=9 上を動くとき，２定点 A(−3 , 0) , B(3 , 0) と点 Q とで作られる△ABQ の重心 P の軌跡を求めよ．
(x−)2+y2=

ただし，点 ( , ) , ( , ) を除く．

採点する やり直す ヘルプ
［例題4］　［２交点の中点の軌跡］
　円 x2+y2=4 と直線 y=x+k とが異なる２点 P , Q で交わるとき，P , Q の中点 M の軌跡を求めよ．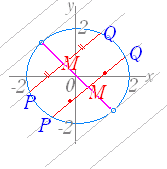
［解答］
点 P , Q の座標を (α , α+k) , (β , β+k)，点 M の座標を (x , y) とおく．
　円 x2+y2=4 と直線 y=x+k の交点が P , Q だから，α，β は，次の連立方程式の解の x 座標
____________x2+y2=4
____________y=x+k
すなわち，２次方程式
____________x2+(x+k)2=4 …(1)
の解が α，βとなる．
(1)より
____________2x2+2kx+(k2−4)=0 …(2)
解と係数の関係により
_____________α+β=−k
_____________αβ=

　 M は，P , Q の中点だから
____________x= =− …(3)
____________y=x+k …(4)

(3)(4)よりk を消去する．
____________y=x+(−2x)=−x …(5)
ただし，２点で交わるのは(2)が異なる２つの実数解をもつときだから， D’=k2−2(k2−4)>0 より
____________k2<8
__________−2<k<2 …(6)
ゆえに，求める軌跡は y=−x の直線のうち，−2<k<2 の部分 …（答）
[公式] 【２次方程式の解と係数の関係】
　２次方程式 ax2+bx+c=0 （ただし a≠0 ）の２つの解を α，β とするとき
_____________α+β=−
_____________αβ=

が成り立つ．これを「２次方程式の解と係数の関係」という．

例
(1)　２次方程式 2x2+3x+4=0の２つの解を α，β とするとき
_____________α+β=−
_____________αβ= 2

(2)　２次方程式 (m+1)x2−2mx+3=0の２つの解を α，β とするとき
_____________α+β=

_____________αβ=

が成り立つ．

[公式] 【判別式】
　２次方程式 ax2+bx+c=0 （ただし a≠0 ）が異なる２つの実数解をもつ条件は
____________D=b2−4ac>0
　特に，x の係数が２の倍数であるときは
　２次方程式 ax2+2b’x+c=0 （ただし a≠0 ）が異なる２つの実数解をもつ条件は
____________D’=b’2−ac>0
例
(1)　２次方程式 2x2+kx+1=0 が異なる２つの実数解をもつ条件は
_____________D=k2−8>0
_____________k<−2 , 2<k
(2)　２次方程式 x2+2kx+1=0 が異なる２つの実数解をもつ条件は
_____________D’=k2−1>0
_____________k<−1 , 1<k
［例題5］　［２交点の中点の軌跡］
　円 (x−2)2+y2=3 と直線 y=mx とが異なる２点 P , Q で交わるとき，P , Q の中点 M の軌跡を求めよ．
［解答］
点 P , Q の x 座標を α , β，点 M の座標を (x , y) とおく．
____________(x−2)2+y2=3
____________y=mx
より
____________(x−2)2+(mx)2=3
____________(m2+1)x2−4x+1=0 …(1)
　 M は，P , Q の中点だから
____________x= = , y=

これらから m を消去する．
（必ずしも m について解かなくてもよい．
とにかく m を消去することを考える． ）
____________x2+y2= ()2+()2

____________===2x

すなわち，(x−1)2+y2=1 の円

ただし，２点で交わるのは(1)が異なる２つの実数解をもつときだから， D’=4−(m2+1)=3−m2>0 より
____________−<m<　→　<x≦2 …(*)
これは元の円の内部にある部分を表わす．
ゆえに，求める軌跡は (x−1)2+y2=1 の円のうち，元の円の内部にある部分 …（答）
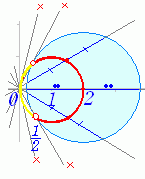円と直線が異なる２点で交わるときだけ中点が決まる．それは軌跡のうちで元の円の「内部」（周上を含まない）にある部分になる．

(*)の変形は難しい：
____________−<m< →　0≦m2<3　→　1≦m2+1<4

____________<x= ≦

____________<x≦2
○===メニューに戻る
■［個別の頁からの質問に対する回答］[軌跡の方程式２について／17.1.11］
問題３のヘルプの下から２行目 「(s , t)=(3 , 0) のとき (x , y)=(2 , 0)」は間違っていて、正しくは 「(s , t)=(6 , 0) のとき (x , y)=(2 , 0)」ではありませんか?
＝＞［作者］：連絡ありがとう．訂正しました．