|
���M�Z�����ʼn������
�@�����w�Z�Ŋw�K���Ă���Ƃ��́C���ȏ��̊����ɂ��Ă���O�p���\�����邱�Ƃ��ł��܂����C����R���s���[�^�����p���邱�Ƃ��ł��܂��D������C���ʂ̏ł́Csin46���Ƃ�cos12���̂悤�Ȋo���Ă��Ȃ��p�x�̎O�p��̒l�ł����R�Ɏg����i�����������_�ȉ���S�ʂ܂ł̏����̒l�j���ƂɂȂ��Ă��܂��D
�@����ɑ��Đ��w�̎����̏ꍇ�ɂ́C���ɋ�����Ȃ����萔�\��R���s���[�^�C�g�ѓd�b�͎������߂Ȃ��̂����ʂł��D���̂悤�ɁC���Z�����ł��悭�ł�����ʂł́C���́u�M�Z�����v�ʼn����Ȃ���Ȃ�܂���D �@���̂悤�ɐ��w�̎����̂悤�Ɂu�M�Z�����ʼn����Ȃ���Ȃ�Ȃ����v�ł�sin75���Ccos105���̂悤�Ȓl�́C�o���Ă��Ȃ�����g���Ȃ����ƂɂȂ�܂��D �@�����ŁCsin75���Ccos105���Ȃǂ̒l���K�v�ɂȂ�����C�ʂ̊p�x�𗘗p������@��T���܂�. �@���̂Ƃ��ɗp��������̂ɂ́C�u�����藝�v�u�]���藝�v�̑��C�]���藝�łQ���������������@�C���]���藝�C�O�p�`�̓��p�̘a������܂�.
��2����2�{��2�|�Q�����E�������a�@�Ȃ�
�m���]���藝�Ƃ́n
�@���̐}�̂悤�ɁC�`���琂�����Ђ��ƁC a=bcosC+ccosB �����藧�D �@��������ɓ��ꊷ����C b=ccosA+acosC c=acosB+bcosA �������܂��D �@��������]���藝�Ƃ����܂��D 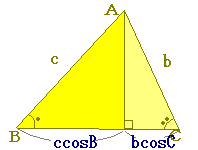 �@���]���藝�́C1�̕�(��)�̑傫�������߂邽�߂ɁC�ӂ̒����Q�C�p�̑傫���Q��K�v�Ƃ��邽�߁C�]���藝�����u�ア�v�藝�ł����C�p�`�̒l�����p�ł��Ȃ��悤�ȏꍇ�ɗL���ł�. �@���̊W����]���藝�C(�ʏ�p����)�]���藝�̂��Ƃ���]���藝�ƌĂԂ��Ƃ�����܂�.
�y���f�̃|�C���g�z
���]���藝���P�]���藝�ŕӂ����߂邽�߂ɂ́C���̕ӂ��Q�������Ă��Ȃ���Ȃ�܂���D a2=b2+c2−2bc cos A b2=c2+a2−2ca cos B a=bcosC+ccosB ���ӂ̒������P����������Ȃ��Ƃ��Ɏg����̂͐����藝�ł��D |
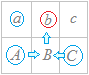 �E�}�̂悤�ɁC
�E�}�̂悤�ɁC