|
�i���Q�l���j�\�v�Z�\�t�g��p�����t�s��̌v�Z
����(A)�`(D)���g���āC�t�s����v�Z������@���������
(A) PC�ɃC���X�g�[�����Ďg��Excel(2007,2010�ȂNj���)
(B) �����Ŏg����Excel Online (C) �����Ŏg����Google�X�v���b�h�V�[�g (D) �����Ŏg����wxMaxima |
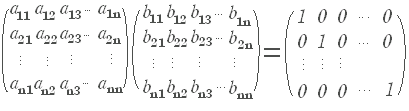 ���@���~���s��ɂ��Ă͋t�s��̗L�����l���邱�Ƃ��ł��܂��D�����s��łȂ���t�s����l����]�n�͂���܂���D ���@���~���s��ɂ��Ă͋t�s��̗L�����l���邱�Ƃ��ł��܂��D�����s��łȂ���t�s����l����]�n�͂���܂���D���@��ʂɂ��~���s�� A �ɁC�E����|���Ă�������|���Ă������̒P�ʍs��ƂȂ邎�~���s�� B �� A �̋t�s��Ƃ����CA- 1 �ŕ\�킷�D�i AB=En �Ȃ�� BA=En �����藧�̂ŁC�E�̂悤�� AB=En �����藧�Ă�B �� A �̋t�s��Ƃ�����D�j |
|
(A)Excel �ɂ͋t�s������߂�� =MINVERSE() ���p�ӂ���Ă���D���̊���p���ċt�s������߂���@���������D �@�i=MINVERSE()�ŋ��߂��P�̎���z��ɒ����Ƃ��ɁC���ӂ��ׂ��_�����������D���ꂳ���ł���Ή��ł��Ȃ��D�j �@�@��ʂɁC�u�s�̒l��0�łȂ��v�u�����s��v�ɑ��Ă͋t�s���݂���D�i�ȉ��̑����Excel2007�C2010�ɋ��ʁD���ʂ͒ʏ�C�����ŕ\������邪�C������₷���悤�ɋt�s��̊e�����������ƂȂ����I�D�j
�@(1)�@�Z�� D1 ���|�C���g���Ă����D �@(2)�@��ʏ�̕��ɂ��鐔���o�[�ɂ��� fx �Ƃ����Ƃ�����N���b�N����Ɓu���̑}���v�ɂȂ�D �@(3)�@�m���̕��ށn�́u���ׂĕ\���v�ɂ��CMINVERSE ��I������DOK
• �u�菑����=MINVERSE( �Ə����v
�@(4)�@�z��Ƃ����\���̋̉E�ɂ���• �u��ʏ���̐����o�[�̍����ɂ��� fx����v�������́u��ʏ�E�̕�����v�v�������I������ꍇ�C�u���̑��̊��v→�u���ׂāv�܂��́u���w/�O�p�v�ɐi�ނ�MINVERSE������i�u����/�s��v�ł͂Ȃ��j �@(5)�@A1����C3�܂Ńh���b�O���CEnter�L�[���������n�j �@�@!! �������炪�d�v !! �ȏ�̑��삾���ł�D1�ɂP�̒l���������܂�邾���ŁC�s��ɂȂ��Ă��Ȃ��D�i���̒l���h���b�O���Ă��_���j �@�@D1����F3�ɔz��i�s��j�Ƃ��Ēl���������ނɂ́F �@(6)�@D1����F3��I�����Ĕ��]�\���ɂ���D �@(7)�@�����o�[�i��قǂ�fx �̉E�ɂ���j�ɐ���=MINVERSE(A1:C3)�����ɏ������܂�Ă���̂ŁC���̗��̂ǂ������}�E�X�Ń|�C���g����D �@(8)�@Ctrl+Shift+Enter�iCtrl�L�[��Shift�L�[�������Ȃ���Enter�L�[�������D�j
|
���Z�F�s��̐ς����߂�ɂ� �@�t�s���������߂��Ă��邩�ǂ������Z����ɂ́C�Q�̐����s��A1�FC3��D1�FF3�̐ς��P�ʍs��E�ɂȂ��Ă��邩�ǂ����ׂ�悢�D�����̍s��̐ς�G1�FI3�ɏ������ނɂ́C �@(1)�@G1���|�C���g���Ă����C��ʏ�[�̐����o�[�̍����ɂ��� fx �Ƃ����Ƃ�����N���b�N����Ɓu���̑}���v�ɂȂ�D �@(2)�@�m���̕��ށn�́u���ׂĕ\���v�ɂ��CMMULT ��I������DOK �@(3)�@�z��1�Ƃ����\���̋̉E�ɂ��� �@(4)�@A1����C3�܂Ńh���b�O���CEnter�L�[���������n�j �@(5)�@�z��2�Ƃ����\���̋̉E�ɂ��� �@(6)�@D1����F3�܂Ńh���b�O���CEnter�L�[���������n�j ��Ɠ��l�C�P�̃Z���̒l������������̂ŁC�����z��i�s��j�ɂ���ɂ� �@(7)�@G1����I3��I�����Ĕ��]�\���ɂ���D �@(8)�@�����o�[�i��قǂ�fx �̉E�ɂ���j�ɐ���=MMULT(A1:C3,D1:F3)�����ɏ������܂�Ă���̂ŁC���̗��̂ǂ������}�E�X�Ń|�C���g����D �@(8)�@Ctrl+Shift+Enter�iCtrl�L�[��Shift�L�[�������Ȃ���Enter�L�[�������D�j ���@�ȏ�ŁCG1�FI3�ɏ�̍s��iA1�FC3�j�ƍs��iD1�FF3�j�̐ς��������܂��D���ꂪ�P�ʍs��ɂȂ��Ă���悢�D �� �R���s���[�^�ɂ�鏬���v�Z�͋ߎ��l�ōs����̂ŁC���w�̋��ȏ��ŏK���悤�Ȃ��ꂢ�ȕ\���ɂ͂Ȃ�Ȃ��F�Ⴆ�C1��3�~3=0.99999··· �ƂȂ邪�C�����1��\�킷�D��̌��Z�ɂ����āC�ʏ�͐����Ƃ͂Ȃ�Ȃ��̂ŁC�Ίp�������C0.99999··· �i��1�ɏ\���߂����j�C�Ίp�łȂ������� 1.01E-13=1.01�~10-13 �i��0�ɏ\���߂����j�ȂǂƂȂ�Ƃ��́C�P�ʍs���\�킵�Ă��邱�Ƃ�����D |
(B)Excel Online���g���ꍇ
���Ȃ킿 �@(1)�@�Z�� D1 ���|�C���g���Ă����D �@(2)�@��ʏ���̐����o�[�̍����ɂ��� fx �Ƃ����Ƃ�����N���b�N����Ɓu���̑}���v�ɂȂ�D �@(3)�@�m���̕��ށn�́u���ׂĕ\���v�ɂ��CMINVERSE ��I������D
• �u�菑����=MINVERSE( �Ə����v
�@(4)�@A1����C3�܂Ńh���b�O���CEnter�L�[������
• �u��ʏ���̐����o�[�̍����ɂ��� fx����v�������́u��ʏ�E�̕�����v�v�������I������ꍇ�C�u���̑��̊��v→�u���ׂāv�܂��́u���w/�O�p�v�ɐi�ނ�MINVERSE������i�u����/�s��v�ł͂Ȃ��j
• �����܂łŁC�E�̕\4�̂悤��D1:F3�͈̔͂ɋt�s�������܂�饥�(A)��Excel�ŕK�v�ł������z��ɂ����Ƃ͕s�v�D • ���̂悤�ɁCExcel Online���� MINVERSE()�����g���ċt�s������߂�Ƃ��́C�t�s���s����ł��邩�Ƃ������Ƃ�m��Ȃ��Ă��ł������ɁC�t�s����������ނׂ��Z���͈̔͂ɁC�ق��̃f�[�^����ɏ������܂�Ă���ꍇ�́C#�X�s��!�i�u���ӂ��v�u���ڂ��v�Ƃ����Ӗ��j�Ƃ��G���[���b�Z�[�W���\������Ď~�܂�D |
(C)Google�X�v���b�h�V�[�g���g���ꍇ �@�����(B)��Excel Online�Ƃقړ����ł��邪�C���j���[����������ǂ�ꍇ�́C�r���o�߂������Ⴄ�D���Ȃ킿
(1) �Z�� D1 ���|�C���g���Ă����D (2)�u�菑����=MINVERSE( �Ə����v (3) A1����C3�܂Ńh���b�O���CEnter�L�[�������D
D1���|�C���g���Ă���C(2)��=MINVERSE()�������j���[�����ǂ��ď������ނɂ�
�@Excel Online�Ɠ��l�ɁCMINVERSE()�����g���ċt�s������߂�Ƃ��́C�t�s���s����ł��邩�Ƃ������Ƃ�m��Ȃ��Ă��ł������ɁC�t�s����������ނׂ��Z���͈̔͂ɁC�ق��̃f�[�^����ɏ������܂�Ă���ꍇ�́C#REF!�Ƃ��G���[���b�Z�[�W���\������Ď~�܂�D
• �}��→��→���ׂ�→MINVERSE �������́C�}��→��→�z��→MINVERSE �������́C��ʏ�E�̕�����v→���ׂ�→MINVERSE �������́C��v→�z��→MINVERSE ���b����₱�������C(A)(B)��Excel�ƈ���āC���̕��ލ��ڂ��u���w�v�ł͂Ȃ��u�z��v�ɂ���D����ɋC�t���Ȃ���C�u���ׂāv����I�Ԃ��ƂɂȂ�D |
|
�����1 �@���̊e�s��ɂ��ċt�s������߂�D�i�M�Z�ōs���C(A)(B)(C)�����ꂩ�̕\�v�Z�\�t�g�Ō��Z����Ƃ悢�D�j (1)
|
�i���j
|
||||||||||||||||||||||||||||||||||||||||||||||||||
(2)
|
�i���j
|
||||||||||||||||||||||||||||||||||||||||||||||||||
(3)
|
�i���j
|
||||||||||||||||||||||||||||||||||||||||||||||||||
(4)
|
�i���j
|
|
�@�����̓ǎ҂́C�t�s��̐������u�����v��u�����v�ł���Ƃ��̎�舵���ɂ��ẮC����Ă���ƍl������̂ŁC�����ł͓��ɏq�ׂȂ��D �t�s��̐�����
�s�ꗗ�t�u�����v�u�������v�u���f���v�u�������v�ł���Ƃ��C�M�҂̍l���ł́C�T�ˎ��̂悤�ɂ܂Ƃ߂���D
|
|
| �@�j �����������ɂȂ�Ƃ� �@�s��̐����̂�������������ɂȂ�Ƃ��CExcel�̏����ݒ�̂܂����\���i�܂��͎w���\���j�ɂ��Ă����ƁC�ǂ̂悤�ȕ�����\�킵�Ă���̂��悭������Ȃ����Ƃ�����D �@���̂Ƃ��C�\���`���Ƃ��āu�����v��I�ԂƁC�����Ƃ��ĕ\���ł���D
�� ����������̏ꍇ���C���q�̕�����������傫�������ƂȂ�ꍇ�́C�������ł͂Ȃ��ѕ����ŕ\�������D
�� �����������̌`�̕����ŁC���ꂪ3���ȉ��̐����ŕ\����ꍇ�́C(A)(B)(C)�̂�����ōs���Ă��C�������ʂ�������D�������C(C)�ł́C# ???/???�����ł́C�}�C�i�X�̕�����\���Ȃ��̂Œ��ӥ��(A)(B)�ƈႤ �� �����������̌`�̕����ŁC���ꂪ4���ȏ�i�Ƃ����Ă����ۏ��6, 7���ȓ��j�̐����ŕ\����ꍇ�́C(B)�ł�3���܂ł̋ߎ������ŕ\�������D(A)(C)�ł͕���̌�����傫���ł��邪�C����ł��Ȃ��C���m�Ȓl���������ɋߎ��l�ƂȂ�Ƃ��́C(C)�̕����ŗNjߎ������ƂȂ邱�Ƃ������D |
�m�菇�n (A)(B)�̏ꍇ
�t�s������炩���ߋ��߂Ă����D�������\���ɂ������Z�����h���b�O���Ĕ��]�\���ɂ���
���������Z�����i�\���`���j���ށF�����C��ށF3���������n�j
�@(A)PC�ɃC���X�g�[�����Ďg��Excel��(B)Excel Online�Ő��l�̕����\����I�ԂƂ��u1�������v�u2�������v�u3�������v�Ƃ���������I�Ԃ��ƂɂȂ邪�C���́u�����v�͂��Ԃ���Łu1���܂Łv�u2���܂Łv�u3���܂Łv�Ƃ����Ӗ��ł���D
���ꂪ3���܂ł̐�����Ƃ��镪���ł͕\���ł��Ȃ��Ƃ��C�i4���C5���C������K�v�ȏꍇ�j(B)�̏ꍇ
3���܂ł̋ߎ������ɂȂ�
�y��z
|
|||||||||||||||||||||||||||||
|
(A)�̏ꍇ
�Z���̏����ݒ�→�\���`��→���[�U�[��`�F��ނ��菑���ŏ��������� # ????/???? �Ƃ����4���܂ŁC# ?????/????? �Ƃ����5���܂ŁC����ƕ\��������ύX�ł���D�i4���܂łŎ��̕\�̂悤�ɂȂ�j
(C)�̏ꍇ
�\���`��→����→�J�X�^���\���`���F�菑���ŏ��������� # ????/????;-# ????/???? �Ƃ����4���܂ŁC# ?????/?????;-# ?????/????? �Ƃ����5���܂ŁC����ƕ\��������ύX�ł���
�i�Z�~�R�����ŋ���āC���̏ꍇ -# ????/????��lj�����K�v������D�����ӂ�ƁC�}�C�i�X�̏ꍇ�ɕ������\������Ȃ��j 4���܂ł�(A)�̕\�Ɠ����ɂȂ�D
�ߎ������Ɋւ��āCExcel��Google�X�v���b�h�V�[�g�̑���_�ɂ��āC�M�ʂ̍l���́C�˂��̃y�[�W�̌㔼�ɂ܂Ƃ߂Ă���܂��D
|
�����2 �@���̊e�s��ɂ��ċt�s������߂�D
(1)
�i���j
(2)
�i���j
(3)
�i���j
|
|
�A�j �t�s��̐������������i�����j�C���f���C�������ɂȂ�Ƃ� �����̏ꍇ�́C(A)(B)(C)�̂����������������C(D)�ōs���Ƃ悢�D 1. �������i�����j���܂ޏꍇ
�y��1.1�z�̂Ƃ��C wxMaxima�ŁC�㐔→����͂ɂ��s��̐���→�s��2�C��2�C�^�C�v�F��ʁC�ϐ����FA�ȂǂƂ��� →������ �@sqrt(2)+1�@sqrt(3) �@−sqrt(3)�@sqrt(2)−1 �Ɩ��߂�D �t�s������߂����invert()�Ȃ̂ŁCinvert(A)�ƋL�����āCShift+Enter |
�@�������ݓ��������ʂ��\�������̂ŁC���̕ό`→���̐����Ƃ���ƁC �ƂȂ��āC�t�s�������D �y��1.2�z�@���l�ɂ��āC���̂悤�ɋt�s���܂�D �y��1.3�z�@���l�ɂ��āC���̂悤�ɋt�s���܂�D |
|
2. ���f�����܂ޏꍇ
�y��2.1�z�̂Ƃ��C wxMaxima�ŁC�㐔→����͂ɂ��s��̐���→�s��2�C��2�C�^�C�v�F��ʁC�ϐ����FB�ȂǂƂ��� →������ �@sqrt(6)�@2−%i �@2+%i�@sqrt(6) �Ɩ��߂�D�i�����P�ʂ�%i�܂���%j�ŕ\���j �t�s������߂����invert()�Ȃ̂ŁCinvert(B)�ƋL�����āCShift+Enter |
�@�������ݓ��������ʂ��\�������̂ŁC���̕ό`→���̐����Ƃ���ƁC �@sqrt(6)�@%i−2 �@−%i−2�@sqrt(6) ���Ȃ킿 �ƂȂ��āC�t�s�������D �y��2.2�z�@���l�ɂ��āC���̂悤�ɋt�s���܂�D �y��2.3�z�@���l�ɂ��āC���̂悤�ɋt�s���܂�D |
|
3. ���������܂ޏꍇ
�y��3.1�z�̂Ƃ��C wxMaxima�ŁC�㐔→����͂ɂ��s��̐���→�s��2�C��2�C�^�C�v�F��ʁC�ϐ����FC�ȂǂƂ��� →������ �@x−3�@2 �@2�@x �Ɩ��߂�D �t�s������߂����invert()�Ȃ̂ŁCinvert(C)�ƋL�����āCShift+Enter ���Ȃ킿 �ƂȂ��āC�t�s�������D �@�������C�t�s���݂��邽�߂ɂ́C�s������0 �� x��−1, 4�������ɂȂ�D |
�y��3.2�z�@���l�ɂ��āC���̂悤�ɋt�s���܂�D �@�������C�t�s���݂��邽�߂ɂ́C�s������0 �� x��2�������ɂȂ�D �y��3.3�z�@���l�ɂ��āC���̂悤�ɋt�s���܂�D �@�������C�t�s���݂��邽�߂ɂ́C�s������0 �� x��0�������ɂȂ�D |
|
���m�ʂ̕ł���̎���ɑ���n[�t�s��Ƃ��ɂ��ā^17.2.8�n
EXCEL�̑��삪��ς킩��ɂ����ł��B���������ł͂Ȃ��A���������Ƃ悢�ł��B���͑���𗝉�����̂ɁA�}�C�N���\�t�g�̃T�|�[�g���g���A����������A���̂��ƁA�������K���āi�L�[���O�����̂��ނ��������Ƃ�����j����Ƃł���悤�ɂȂ�܂����A
���m�ʂ̕ł���̎���ɑ���n[�t�s��Ƃ��ɂ��ā^17.2.8�n
�����m��ҁn�F�A�����肪�Ƃ��D������̕ԐM�̕�����Ȃ̂ŁC���������悤�ł悩�����ł��D ����Ƃ����̂�1�̉�����ł����C�M�҂͊��Ȃ܂肪�����Ƃ��炩���邱�Ƃ������̂ŁC���ݓ���ɂ���\��͂���܂���D �������Ă����܂��G�N�Z���ŕ\������܂���(EXCEL2013)�B���̗����������̂ł��傤���B�r���ɂ���Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D |