|
[要点]
■連立1次方程式 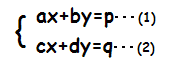 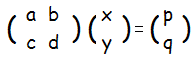 すなわち,A= 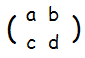 ,X= ,X=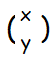 ,P= ,P=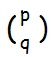 とおくと, とおくと,
■方程式 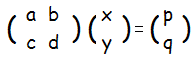 は, は,
(ア) Δ=ad−bc≠0のとき,ただ一つの解を持ち, i) (1)//(2)のとき 解なし |
※補足説明
一つの行列の等式は,その成分数だけの連立方程式と同じです。 例1: 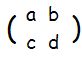 = =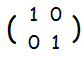 は,連立方程式 は,連立方程式
例2: 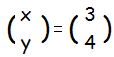 は,連立方程式 は,連立方程式
例3: 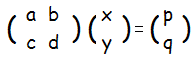 は,左辺を計算して2×1行列にしておくと は,左辺を計算して2×1行列にしておくと
|
|
[要点]
■連立1次方程式 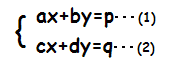 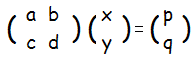 すなわち,A= 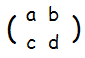 ,X= ,X=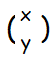 ,P= ,P=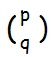 とおくと, とおくと,
■方程式 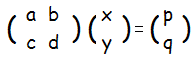 は, は,
(ア) Δ=ad−bc≠0のとき,ただ一つの解を持ち, i) (1)//(2)のとき 解なし |
※補足説明
一つの行列の等式は,その成分数だけの連立方程式と同じです。 例1: 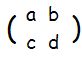 = =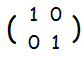 は,連立方程式 は,連立方程式
例2: 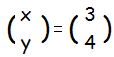 は,連立方程式 は,連立方程式
例3: 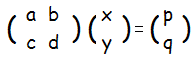 は,左辺を計算して2×1行列にしておくと は,左辺を計算して2×1行列にしておくと
|
(ア) 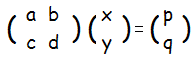 の両辺に左からA-1を掛けると, の両辺に左からA-1を掛けると,
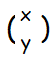 = =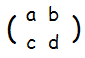 -1 -1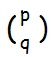
これを成分に分ければ解となります。 (イ) Δ=0のとき,行列ではこれ以上変形できないので,成分に分けます。
|
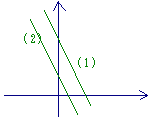
|
[例題] 逆行列を用いて,次の連立方程式を解きなさい。
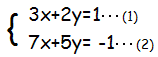 |
[答案例]
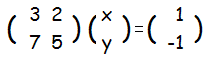
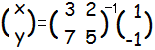 = =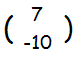
x=7,y=-10・・・答
|
[例題] 次の連立方程式を解きなさい。
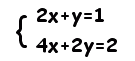 |
[答案例]
Δ=4-4=0 2x+y=1 の辺々2倍すると 4x+2y=2 と一致するから, 2x+y=1 を満たすx,yは 両方の方程式を満たす。 2x+y=1を満たす(x,y)はすべて解・・・答
[直線2x+y=1上の点・・・答] [x=t,y=1-2t (tは実数)・・・答] |
[例題] 次の連立方程式を解きなさい。
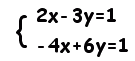 |
[答案例]
Δ=12-12=0 2x-3y=1 → -4x+6y=-2・・・(1) 条件より -4x+6y=1 ・・・(2) (1)(2)を両方満たすことはできないから, 解なし・・・答
|
1
 |
 |
|
2
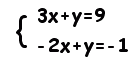 |
 |
|
3
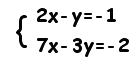 |
 |
|
【付録1】…2元連立1次方程式(未知数2個,方程式2個のもの) 各自で確かめたい連立方程式を書き込んでください.(空欄を移動するにはTabキーが使えます)
ただし
• 整数係数の問題に限ります. • 解がただ一つに定まる問題に限ります.(不能解・不定解となる問題は扱っていません) |
||
|
|
|
|
|
【付録2】…3元連立1次方程式(未知数3個,方程式3個のもの) 各自で確かめたい連立方程式を書き込んでください.(空欄を移動するにはTabキーが使えます)
ただし
• 整数係数の問題に限ります. • 解がただ一つに定まる問題に限ります.(不能解・不定解となる問題は扱っていません) |
||
|
|
|
|
| ○ Excelを使って連立方程式を解く方法は⇒この頁 |
|
■[個別の頁からの質問に対する回答][行列と連立方程式について/17.7.27]
例題が間違ってると思う。
■[個別の頁からの質問に対する回答][行列と連立方程式について/17.6.2]
=>[作者]:連絡ありがとう.?? 例題が間違っているということはないでしょう.例えば,例題の解答が間違っているとか,例題の問題の符号が間違っているというような場合はあり得ますが・・・ところで,あなたは不定解や不能解が出る連立方程式は,問題が間違っていると考えていませんか. 付録中の代入式の中で、かっこが斜めっているのは解せん。
=>[作者]:連絡ありがとう.筆者はどちらでもよいと思いますが,とりあえず直立にしました. |