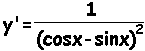|
== 三角関数の導関数 ==
■三角関数の導関数を求めるためには,次の極限値を用います。 ■これにより 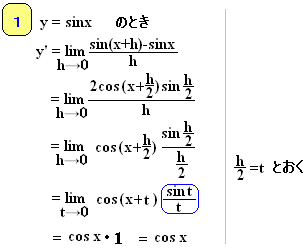 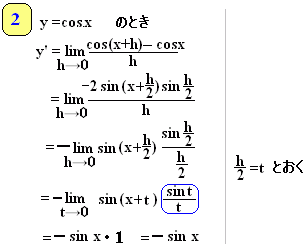 y=tanxのときはsinx,cosxの結果を用いて商の微分法で求められます。 |
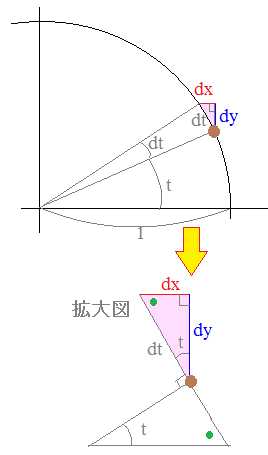 (参考)
(参考)半径1の円(単位円)上の動点P(x,y)を考えると y=sint x=cost 角度がtからdtだけ増えたとき 右図の茶色で示した点から接線に沿って(弧の長さ≒斜辺の長さ)dtの直角三角形を描くと 緑で示した角が平行線の錯角で等しいから,この直角三角形の1つの角はtになる (1) (2) 次に,図のようにtが第1象限の角の場合,tが増えるとxは減少する.そこでdxの符号は負になる. ※この図は,第1象限の場合しか示せていないので,証明としてはやはり上に示した極限値を使った式で行う方がよい. [まとめ]  |
 ・・答
・・答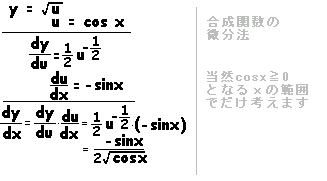 ・・答
・・答