|
■積の法則 右図1のように、P地点からQ地点に行く道が3通りあって、「その各々について」Q地点からR地点に行く道が2通りあるとき、P地点からQ地点を通ってR地点に行く道は 一般に、次の法則が成り立ちます。
(積の法則)
Aの起こり方がm通り、その各々についてBの起こり方がn通りあるとき、AもBも起こる場合の数は m×n通りになります。
■積の法則を使うかどうかの見分け方■
「各々何通り」あるときに、「AかつBが起こる」場合の数を求めるのは「積の法則」
【例1】
りんご、かき、みかんが各1個、計3個あるとき、この中から2個選んで前後1列に並べる方法は何通りありますか。  (解答) (解答)前に置く果物は、りんご、かき、みかんのどれでもよいから3通り。 その各々について、(残りは2個になっているから)後に置く果物の選び方は2通り。 積の法則により,3×2=6通り・・・(答)
【例2】
2桁の正の整数のうちで、十の位の数が奇数で、一の位の数が偶数となる数は何通りありますか。  (解答) (解答)十の位の数の決め方は、1,3,5,7,9の5通り その各々について、一の位の数の決め方が、0,2,4,6,8の5通りあるから |
図1

【例3】
赤、青、黄、緑、茶色の5色のうち異なる4色を使って、次の図のア〜エを塗る方法は何通りありますか。 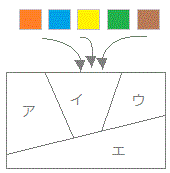 (解答)
(解答)アの塗り方は5通り その各々についてイの塗り方は(アで使った色以外の)4通り その各々についてウの塗り方は(ア、イで使った色以外の)3通り その各々についてエの塗り方は(ア、イ、ウで使った色以外の)2通り 積の法則により、
【例4】
18(=2×32)の正の約数は何個ありますか。(1と18自身も含めて数えるものとします。)
18の正の約数は2○×3□の形に書けます。 ○には0,1の2通りの入れ方があり、その各々について□には0,1,2の3通りの入れ方があります。(20=1,30=1です) (2○×3□の形の積は右の表の通り) |
||||||||||||
|
問題1次の立方体ABCD-EFGHにおいて,頂点AからGへ遠回りをせずに辺をたどっていく方法は何通りありますか.(図の赤線はそのうちの1つの例です)
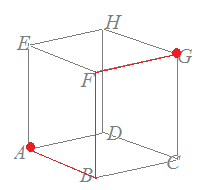 Aから進む方法はA→B, A→D, A→Eの3通り
Aから進む方法はA→B, A→D, A→Eの3通りその各々について次の進む方が2通り その各々についてGに進む方法が1通りだから 積の法則により,AからGへ進む方法は3×2×1=6通り 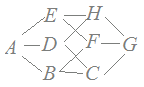 |
問題2次の式を展開したとき,何個の項ができますか.
展開とは「代表選手の選び方」だと考えるとよくわかります.例えば,次の図のように左の( )から1つの項bを,中央の( )から1つの項sを,右の( )から1つの項wを選んで組み合わせるとbswができます.1つの( )からは「代表選手は1つだけ」えらぶことができ,abなどという項はできません. 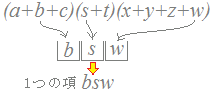 積の法則により,3つの( )から代表選手を選ぶ方法は3×2×4=24通り |
||||||||||||
|
問題32桁の偶数は何個ありますか.(例えば10, 24は2桁の偶数ですが04は最高位の数が0なので,2桁ではなく1桁と考えます.)
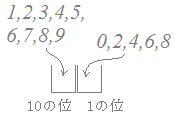 10の位の選び方は1から9までの9通り(0はダメ)
10の位の選び方は1から9までの9通り(0はダメ)偶数だから,その各々について1の位の選び方は0, 2, 4, 6, 8の5通り 積の法則により,9×5=45通り (2桁の整数は10から99まで,99−10+1=90個[両端を含める植木算になるので+1]ありますが,そのうちの半分が偶数です.) |
問題4720の正の約数は何個ありますか.
720=24×32×5の約数は
例えば,22×31×51=60
そこで,2の指数xの選び方が5通り,その各々について3の指数yの選び方が3通り,その々について5の指数zの選び方が2通り指数(肩に付いている数)が0となる場合については数Aではまだ習いませんが数IIで習うように1を表します.
20=1, 30=1, 50=1
・20×30×50=1いずれも0ではありませんので注意 ・21×30×50=2 ・22×31×50=12 … ・24×32×51=720 積の法則により,5×3×2=30通り
一般に,p,q,rが素数,a,b,cが0以上の整数であるとき
(簡単な受験問題としてよく出る問題です.) |
||||||||||||
|
問題5108の正の約数は何個ありますか.
108=22×33の約数は(2+1)×(3+1)=12個
20×30=1, 20×31=3, 20×32=9, 20×33=27
21×30=2, 21×31=6, 21×32=18, 21×33=54 22×30=4, 22×31=12, 22×32=36, 22×33=108 |
問題672の正の約数の総和は幾らになりますか.
72=23×32の約数は次に =(8+4+2+1)(9+3+1)=15×13=195 |
||||||||||||
|
問題79138のように各位の数がすべて異なる4桁の正の整数は何個ありますか.
千の位は0以外だから9通りその各々について,百の位は千の位に使われた数字を除いてたもの(ただし千の位以外は0もよい)だから9通り その各々について,十の位は千の位と百の位に使われた数字を除いたものだから8通り その各々について,一の位は千の位,百の位,十の位に使われた数字を除いたものだから7通り 積の法則により,9×9×8×7=4536個 |
問題84桁の電話番号や暗証番号というときには最高位の数として0が使われることも許されます.4桁の電話番号で各位の数がすべて異なるもので全体で奇数を表しているものは何通りありますか.
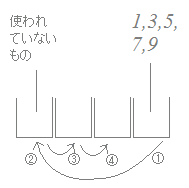 千の位から順に埋めなければならないことはなく,どの位の数から埋めても構いません.このような問題では「条件の厳しい」位から埋めると場合分けが少なくて済みます.
千の位から順に埋めなければならないことはなく,どの位の数から埋めても構いません.このような問題では「条件の厳しい」位から埋めると場合分けが少なくて済みます.一の位は,1,3,5,7,9の5通り その各々について,千の位の埋め方は一の位に使われたものを除いて(この場合は0も許して)9通り その各々について,百の位の埋め方は,一の位と千の位に使われたものを除いて(0も許して)8通り その各々について,十の位の埋め方は,一の位,千の位,百の位に使われたものを除いて(0も許して)7通り 積の法則により,9×8×7×5=2520通り |
||||||||||||
|
|||||||||||||