|
■三角不等式
【例題１】
（最後までたどり着けない答案）0≦θ<2πのとき， cos(2θ−  π3)>√32を満たすθの値の範囲を求めることを考えます． 右上の図は，黒色がy=cosθのグラフ，緑色がy=cos2θのグラフです．
一般にy=cosnθのグラフはy=cosθのグラフを横方向にｎ倍に引き延ばしたものになるのではなく，ｎ分の１に縮めたものになることに注意しましょう
右中央の図は，緑色がy=cos2θのグラフ，青色がy=cos(2θ− π3)すなわちy=cos2(θ−π6)のグラフです．
一般にy=cos n(θ−α)のグラフはy=cos nθのグラフを右にαだけ平行移動したものとなります．
以上のようにして描いたものが３番目のグラフで青色で示した(1) y=cos n(θ−α)のときに右にαだけ平行移動で，y=cos n(θ+α)のときは左にαだけ平行移動となることに注意しましょう． (2) このとき平行移動する分量はy=cos n(θ−α)の形で判断し，y=cos(nθ−α)の形でそのまま読むと間違います．すなわち， y=cos(2θ−  π3)はy=cos2θのグラフを右に π3だけ平行移動したものではなくπ6だけ平行移動したものになります．
y=cos(2θ− π3)のグラフで，赤で示したのがy=√32のグラフです． 青と赤の２つのグラフから，cos(2θ− π3)>√32を満たす範囲は２箇所あるということが分かりますが，実際の答案にまでまとめるのは大変困難です．
▲ 理屈の上では，このようにすれば解けるはずですが，現役の高校生がこの方法で答案をまとめるのは困難です．
▲ 第１の理由は，３番目のグラフを作るまでの作業が長くて，なかなかたどり着けないことです． ▲ 第２の理由は，３番目の青で示したグラフが正確に描けても，このグラフから条件を満たすθの範囲を読み取るのは困難だからです．  ○ 他の解き方を考える方がよさそうです． |
現在地と前後の項目 正の角・負の角/動径の表わす一般角/三角関数の定義 /(第2象限) /(第3象限) /(第4象限) /(まとめ)/弧度法の単位：ラジアン/三角関数の値(よく使う角度)/sin(π+θ)など/三角方程式 /三角不等式/三角関数のグラフ(sinθの平行移動)/(cosθの平行移動)/sin(θ－α)のグラフ（解説）/(振幅)/(周期)/(周期と振幅)/三角関数のグラフ(総合1)/三角関数のグラフ(総合2)/加法定理，倍角公式，３倍角公式，半角公式/加法定理の練習問題/２倍角公式.半角公式/加法定理の数値計算/積和.和積の公式/練習問題2/練習問題3/練習問題4/合成公式/三角不等式/三角関数（まとめ）/[センター]積和の公式/[センター]合成公式/三角関数公式一覧/三角関数公式プラス/三角形の証明・形状問題/センター試験.三角関数(2015年～)/ |
||||
|
（答案） 単位円を使って考える． 0≦θ<2πのとき，t=2θ− π3とおくと
←≪定義域の変換≫ 右図の青で示した円（重ならないように少しだけずらして示 している）は，− π3≦t<11π3となるtについての図とします．図から，cost> √32となるtの値の範囲は− π6<t<π6…（１順目）11π6<t<13π6…（２順目）これをθの範囲に直すと − π6<2θ−π3<π611π6<2θ−π3<13π6θについて解くと π12<θ<π4, 13π12<θ<5π4…（答）
○ このように単位円を使って解くときは，特に≪定義域の変換≫に注意しなければなりません．
○ 元のθが１周している場合でも，新しい変数tでは２周する場合もあります．（円が重ならないように描けばよいでしょう） ○ cosθ, costの値はx座標で調べます．sinθ, sintの値はy座標で調べます． |
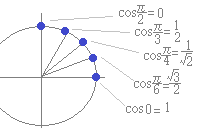※π6とか11π6のような角度はどこから出てくるのか？ ⇒重要な5つの角度の正弦・余弦の値は「覚えているから」できるのです． （上下左右対称に応じてこれに符号を付けます） |
||||
|
【例題２】
（解答）0≦θ<2πのとき， sin(2θ+ π4)≦√22を満たすθの値の範囲を求めてください． t=2θ+ π4とおくと
0≦θ<2πのときπ4≦t<17π4…(1)この範囲でsint≦ √22…(2)を解く．右図より t= π43π4≦t≦9π411π4≦t<17π4
(1)(2)とも等号がある値は解に含まれる
θで表すと2θ+ π4=π43π4≦2θ+π4≦9π411π4≦2θ+π4<17π4したがってθ=0, π4≦θ≦π, 5π4≦θ<2π…（答）
|
|
問１ 0≦θ<2πのとき，
1cos(2θ+ π2)<−12を満たすθの値の範囲を求めてください． 2π3<θ<4π3, 8π3<θ<10π32 π6<θ<5π6, 13π6<θ<17π63 π12<θ<5π12, 13π12<θ<17π124 11π12<θ<19π12, 23π12<θ<2πHELP |
t=2θ+
π2とおくと
0≦θ<2πのときπ2≦t<9π2この範囲でcost<− 12を解く．右図より 2π3<t=2θ+π2<4π38π3<t=2θ+π2<10π3θについて解くと π12<θ<5π12, 13π12<θ<17π12 → 3 |
|
問２ 0≦θ≦πのとき，
1sin(3θ− π3)>√22を満たすθの値の範囲を求めてください． π4<θ<3π4, 9π4<θ<8π32 7π12<θ<13π12, 31π12<θ≦3π3 5π36<θ<11π36, 29π36<θ<π4 7π36<θ<13π36, 31π36<θ≦πHELP |
t=3θ−
π3とおくと
0≦θ≦πのとき− π3≦t≦8π3この範囲でsint> √22を解く．右図より π4<t=3θ−π3<3π49π4<t=3θ−π3≦8π3θについて解くと 7π36<θ<13π36, 31π36<θ≦π → 4 |
|
問３ 0≦θ≦πのとき，
1− 12<cos(3θ−π6)≦√22を満たすθの値の範囲を求めてください． π4≦θ<2π3, 4π3≦θ<7π4, 9π4≦θ<8π32 5π12<θ≦5π6, 3π2<θ≦23π12, 29π12<θ≦17π63 5π36≦θ<5π18, π2<θ≦23π36, 29π36≦θ<17π184 11π36<θ≦8π18, 2π3≦θ<29π36, 35π36<θ≦πHELP |
t=3θ−
π6とおくと
0≦θ≦πのとき− π6≦t≦17π6この範囲で − 12<cost≦√22を解く．右図より π4≦t=3θ−π6<2π34π3<t=3θ−π6≦7π49π4≦t=3θ−π6<8π3θについて解くと 5π36≦θ<5π18, π2<θ≦23π36, 29π36≦θ<17π18 → 3 |
|
【例題３】
（解答）0≦θ≦πのとき， tan(2θ− π6)≧1を満たすθの値の範囲を求めてください． t=2θ− π6とおくと
0≦θ≦πのとき−π6≦t≦11π6この範囲でtant≧1を解く． 右図より π4≦t=2θ−π6<π25π4≦t=2θ−π6<3π2θについて解くと， 5π24≦θ<π3, 17π24≦θ<5π6…（答）
【例題４】
（解答）0≦θ≦πのとき， tan(2θ+ 5π6)≦−√3を満たすθの値の範囲を求めてください． t=2θ+ 5π6とおくと
0≦θ≦πのとき5π6≦t≦17π6この範囲でtant≦− √3を解く．右図より 3π2<t=2θ+5π6≦5π35π2<t=2θ+5π6≦8π3θについて解くと， π3<θ≦5π12, 5π6<θ≦11π12…（答）
|
tanθの値は，x座標やy座標ではなくそれらの比になります． すなわち，tanθ= sinθcosθ=yxなので，m=tanθの値は原点
を通る直線y=mxの傾きmになります．
【重要】
○ この値を全部言えなければ問題は解けません． ○ 特に， π2, 3π2のところ（通俗的に言えば「北極」と「南極」
のところ）では，tanθの値は定義されないことに注意．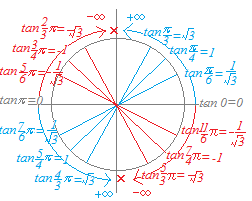
 |
|
問４ 0≦θ≦πのとき，
1tan(2θ+ π3)<−√3を満たすθの値の範囲を求めてください． π12<θ<π6, 7π12<θ<2π32 π6<θ<π3, 2π3<θ<5π63 π4<θ<π3, 3π4<θ<5π64 π2<θ<2π3, 3π2<θ<5π3HELP |
t=2θ+
π3とおくと
0≦θ≦πのときπ3≦t≦7π3この範囲でtant<− √3を解く．右図より π2<t=2θ+π3<2π33π2<t=2θ+π3<5π3θについて解くと π12<θ<π6, 7π12<θ<2π3 → 1 |
...メニューに戻る