|
解説
【an+1=an+f(n)の形の漸化式】
(解説)2項間漸化式が an+1=an+f(n) …(1) の形で与えられているとき,一般項anは an=a1+f(k) …(2) で求めることができます.
※この形の2項間漸化式の特徴はanの係数が1になっているということです.
(1)式をan+1−an=f(n)と変形すると,anの階差数列の第n項すなわち(1)式のように an+1=1an+f(n) となっているときに,この公式を適用します. ※anの係数が1でないときは,他の公式を考えます. bn=an+1−an が bn=f(n) として与えられていることになるから,階差数列から元の数列の一般項を求める公式 an=a1+bk 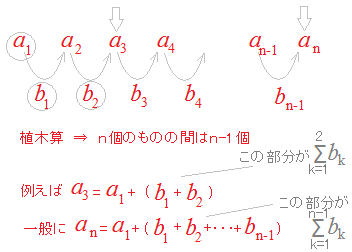 an=a1+f(k) |
※初歩的な注意として,次の点を押さえておきましょう. □ (2)式において,Σ記号の内部では文字nをkに書き換えて使います.したがって,f(n)はf(k)に変わります. an=a1+f(k) □ (2)式において,Σ記号の上に乗っているのはnではなくn−1です.すなわち,このΣは f(1)+f(2)+f(3)+...+f(n−1) を表します. an=a1+f(k) □ (2)式においては階差数列の和だけで元の数列が求まるのではなく,元の数列の第1項も足さなければなりません. an=a1+f(k) □ (2)式は,高校数学におけるΣ記号の使い方の約束として,Σ記号で表される式が少なくとも1つの項を含んでいることを前提としています.だから(2)式はn=1の場合を表しません.そこで,答案では次の例のように,途中経過においてn=1の場合と,n≧2の場合を分けて作成しなければなりません.
(ア) a1=1
ほとんどの場合,結果的にn=1の場合は,n≧2の一般項を「1まで延長した」ものになりますが,そうだからといって「途中経過において分けて求めるという手続きを省略してはいけません.」慣れてくれば,次の例のように別途求めて,結果的に吸収したというスタイルでもよい.
(イ) n≧2のとき an=2n−1 したがって,n≧1のときan=2n−1
運転免許試験で「左右確認しているかどうか」だけをチェックしているのと同様に,採点官はn=1の場合と,n≧2の場合を分けているかどうかだけを見ているので,最後のまとめを「すべての自然数nについて...」と書いていても,「n≧1のとき...」と書いていても,単に「an=2n−1」と書いていてもほとんど気にしていない.したがって,これらのいずれでもよい.
an=2n−1
(n=1のときもこれでよい) |
|
例と答1
≪この形の問題と解答≫
(1)
階差数列を{bn}とおくと
bn=an+1−an=2 a1=3
a1=3an+1=an+2 のとき数列{an}の一般項を求めてください. (ア) n≧2のとき ゆえに,すべての自然数nについて,an=2n+1 …(答)
(初歩的な注意)
2(n−1)になります. 一般にcを定数とするとき, \( \displaystyle \sum_{k=1}^{n}c=cn \) だから \( \displaystyle \sum_{k=1}^{n-1}c=c(n-1) \) です |
(2)
階差数列を{bn}とおくと
bn=an+1−an=3 a1=2
a1=2an+1=an+3 のとき数列{an}の一般項を求めてください. (ア) n≧2のとき ゆえに,すべての自然数nについて,an=3n−1 …(答)
(初歩的な注意) 3(n−1)になります. |
|
(3)
 a1=1
a1=1an+1=an+n−2 のとき数列{an}の一般項を求めてください. |
(4)
 a1=4
a1=4an+1=an+2n+3 のとき数列{an}の一般項を求めてください. |
|
(5)
 a1=1
a1=1an+1=an+n2+1 のとき数列{an}の一般項を求めてください. |
(6)
 a1=2
a1=2an+1=an+n2+3n+2 のとき数列{an}の一般項を求めてください. |
|
例と答2
(7)
 a1=1
a1=1an+1=an+n3 のとき数列{an}の一般項を求めてください. |
(8)
 a1=0
a1=0an+1=an+n(n+1)(n+2) のとき数列{an}の一般項を求めてください. |
|
(9)
 a1=1
a1=1an+1=an+2n のとき数列{an}の一般項を求めてください. |
(10)
 a1=4
a1=4an+1=an+3×2n+1 のとき数列{an}の一般項を求めてください. |
|
(11)
 a1=1
a1=1an+1=an+ のとき数列{an}の一般項を求めてください. |
(12)
 a1=0
a1=0an+1=an+ のとき数列{an}の一般項を求めてください. |
|
問題
【問題】 …(簡単な再現問題=上と同じ問題=です)次の漸化式で定義される数列の一般項を求めてください. 各々正しい選択肢をクリック
(1)
an=2n−3
an=2n+1
an=3n−1
an=3n+2 a1=2
a1=2an+1=an+3 解説
階差数列を{bn}とおくと
bn=an+1−an=3
(ア) n≧2のとき ゆえに,すべての自然数nについて,an=3n−1 …(答) |
(2)
an=(n−1)2
an=n2
an=(n+1)2 a1=4
a1=4an+1=an+2n+3 解説 |
|
(3)
an=(n−1)(n+1)
an=n(n+1)
an=(n+1)(n+2)
an=n(n+1)(n+2)
 a1=2
a1=2an+1=an+n2+3n+2 解説 |
(4)
an=(n−2)(n−3)
an=(n−1)(n−2) a1=0
a1=0an+1=an+n(n+1)(n+2) an=n(n+1)(n+2) an=(n−1)n(n+1)(n+2) 解説 |
|
(5)
an=2n−1
an=2n+1 a1=1
a1=1an+1=an+2n an=2n+1−1 an=2n−1+1 解説 |
(6)
an=1−
an=1+
an=2−
an=2+ a1=1
a1=1an+1=an+ 解説 |
|
|