|
■3次関数(文字係数と極値)
【実習1】
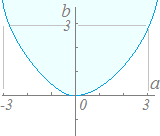
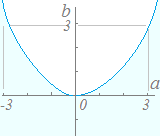
○ 右の≪図1≫において,青で示した曲線は y=x3−x 黒で示した曲線は y=x3 緑で示した曲線は y=x3+x 赤で示した曲線は y=x3+ax…(*) です. ○ 右図の赤で示した縦のスケールを適当にクリックして,(*)の曲線のaの値を変えてください. 
3次関数y=x3+axが極値をもつような定数aの値の範囲は
a<0  a=0の場合は,なんでだめなんだよ〜 
いい質問ですね.あとでゆっくりお話しします.(*)
【実習2】
○ 右の≪図2≫において,青で示した曲線は y=−x2+x 緑で示した曲線は y=−2x2+4x 赤で示した曲線は y=−ax2+(3a−2)x…(**) です. ○ 右図の赤で示した横のスケールを適当にクリックして,(**)の曲線のaの値を変えてください. 
3次関数
y=−ax2+(3a−2)x
が極値をもつような定数aの値の範囲は a<1, 2<a |
aの値
aの値 |
|
≪解説≫
■極大と極小
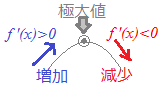 ○導関数f '(x)の符号が正から負に変わるとき,関数f(x)は増加から減少に変化し,その点で極大値をとる.
○導関数f '(x)の符号が正から負に変わるとき,関数f(x)は増加から減少に変化し,その点で極大値をとる.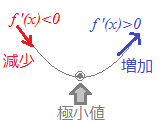 ○導関数f '(x)の符号が負から正に変わるとき,関数f(x)は減少から増加に変化し,その点で極小値をとる.
○導関数f '(x)の符号が負から正に変わるとき,関数f(x)は減少から増加に変化し,その点で極小値をとる.○極大値と極小値を合わせて極値という. ※単にf '(x)=0となっているだけでは,極大値か極小値かわからないだけでなく,極値でない場合がある. 次の図の点Aにおいては,f '(x)=0であるが,その符号は「正→正」だから「符号は変化しておらず,Aでは極値とならない」. 図の点Bにおいても,f '(x)=0であるが,その符号は「負→負」だから「符号は変化しておらず,Bでは極値とならない」. 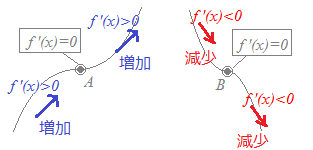  (*)
(*)f '(x)=0だけでは極値とは言えない
≪要点≫
(1)の解説は上で述べた(1) 極値となる条件 微分可能な関数f(x)が,x=pにおいて極値となるための条件は,x=pの前後でf '(x)の符号が変化することである (2) 3次関数が極値をとる条件 3次関数f(x)が,極値をもつための条件は, 2次方程式f '(x)=0が異なる2つの実数解をもつことである
※3次関数が極値をもたないとき,次の2つの場合がある.
・・・(3次の係数が負の場合は「単調減少」と読み替えること)・・・
(ア) ≪図1≫の緑色で示したような 全区間で「単調増加」となっている場合 (イ) ≪図1≫の黒色で示したような, 「1点でのみf '(x)=0」「その両側で単調増加」となっている場合  右の欄に赤で示したように(イ)の場合も「全区間で単調増加」になります. 結局, 「3次関数が極値をもたない場合,全区間で単調増加となります.」 (ア)(イ)いずれの場合でも単調増加ということです.
(2)の解説 3次関数 f(x)=ax3+bx2+cx+d (a>0) の導関数 f '(x)=3ax2+2bx+c について,2次方程式 3ax2+2bx+c=0が ア) 異なる2つの実数解(α,β (α<β))をもつとき,次の表のようにf '(x)の符号の変化する点があるから,極値をもつ. (a<0のときは符号が逆になり,極大・極小も逆になるが,極値はある.)
(a<0のときは符号が逆になるが,同様)
(a<0のときは符号が逆になるが,同様)
|
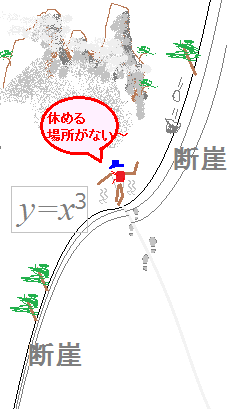 (参考) 数学IIでは,増加・減少をf '(x)の符号で決めることになっていますが,高校数学全体においては次のように代数的に定義することもできます.
a<b ⇔ f(a)<f(b)
が成り立つとき,その区間において単調増加関数であるという.
上で解説したf(x)=x3のグラフは,単に−∞<x<0および0<x<∞の2つの区間で増加であるというだけでなく,−∞<x<∞において増加であるという所が重要です.
a<b ⇔ f(a)>f(b) が成り立つとき,その区間において単調減少関数であるという.
a<b(<0),例えばa=−2, b=−1のとき
さらに,a, bのいずれか一方が0である場合でも,成り立つことが重要です.
f(a)=−8<f(b)=−1は明らかでしょう. (0<)a<b,例えばa=1, b=2のとき f(a)=1<f(b)=8は明らかでしょう. a<0<b,例えばa=−1, b=2のとき f(a)=−1<f(b)=8は明らかでしょう.
a<0, b=0,例えばa=−1, b=0のとき
以上により,a<b ⇔ f(a)<f(b)が成り立つので,全区間−∞<x<∞においてf(x)=x3は単調増加であると言えます.f(a)=−1<f(b)=0が成り立つ. a=0, b>0,例えばa=0, b=1のとき f(a)=0<f(b)=1が成り立つ. (数学の答案としては,
b3−a3=(b−a)(b2+ba+a2)の後ろの因数を平方完成して示すのが普通)
【例題1】
(解答)実習1の問題を次の形にする.
「3次関数y=x3+axが極値をもつような定数aの値の範囲を求めてください.」
y'=3x2+a=0が異なる2つの実数解をもつ条件は 判別式D'=0−3a>0よりa<0…(答)  a=0の場合は,だめです
【例題2】
(解答)実習2の問題を次の形にする.
「3次関数
y=−ax2+(3a−2)x
が極値をもつような定数aの値の範囲を求めてください.」 y'=x2−2ax+(3a−2)=0が異なる2つの実数解をもつ条件は 判別式D'=a2−3a+2>0よりa<1, 2<a…(答)  a=1, 2の場合は,だめです |
||||||||||||||||||||||||||||||||||||
|
【例題3】
(解答)関数f(x)=2x3−6ax2+6x−2が極値をもたないような定数aの値の範囲を求めてください. f '(x)=6x2−12ax+6=6(x2−2ax+1) 2次方程式x2−2ax+1=0について 判別式D'=a2−1≦0より−1≦a≦1…(答)
上で解説したように,D'=0 ⇔ a=±1のときも極値がないことに注意してください.
|
【例題4】
(解答)関数f(x)=x3+3x2+3ax−1がつねに増加となるように定数aの値の範囲を求めてください. f '(x)=3x2+6x+3a=3(x2+2x+a) 2次方程式x2+2x+a=0について 判別式D'=1−a≦0よりa≧1…(答) 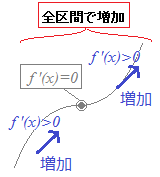
上で解説したように, D'=0 ⇔ a=1 のときも含めて, 「極値がない」→「つねに増加」 となることに注意してください. |
|
正しい選択肢の番号を選んでください. |
導関数を求める
f '(x)=3x2+6ax+(3a+6)=3{ x2+2ax+(a+2) } 2次方程式x2+2ax+(a+2)=0について 判別式D'=a2−a−2>0 (a+1)(a−2)>0 a<−1, 2<a…3…(答) |
|
導関数を求める
f '(x)=6x2−6ax+6=6(x2−ax+1) 2次方程式x2−ax+1=0について 判別式D=a2−4≦0 (a+2)(a−2)≦0 −2≦a≦2…2…(答) |
|
|
導関数を求める
f '(x)=3x2+2ax+b (cは影響しない) 2次方程式3x2+2ax+b=0について 判別式D'=a2−3b>0 b<…3…(答) |
|
|
導関数を求める
f '(x)=3x2+6(a+1)x+6=3{ x2+2(a+1)x+2 } 2次方程式x2+2(a+1)x+2=0について 判別式D'=(a+1)2−2≦0 −≦a+1≦ −1−≦a≦−1+…2…(答) |
|
|
a=0の場合は2次関数になり,増加の区間も減少の区間もできますので,a≠0でなければなりません.
a<0の場合は極値があるときでも,極値よりも外の区間で減少となるので,aは負であってはいけません. 以上により,少なくともa>0でなければなりません.…(1) 導関数を求める f '(x)=3ax2+12x+(3a−9)=3(ax2+4x+a−3) 2次方程式ax2+4x+a−3=0について 判別式D'=4−a(a−3)=−(a2−3a−4)≦0 a2−3a−4≧0 (a+1)(a−4)≧0 a≦−1, 4≦a…(2) (1)(2)より a≧4…3…(答) |