【例2】
直線 x−1==z−2と点 (0, 0, 3)を含む平面
の方程式を求めてください.
いろいろな解き方が考えられます.
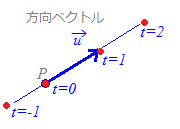
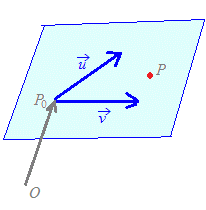
直線は点(1, 1, 2)を通り,方向ベクトル=(1,2,1)に平行だから,右図を参考にすると
(A) 点(0, 0, 3)を通り,2つのベクトル=(1,2,1), =(1,1,−1)を含む平面と考えることができます.
(B) 3点(0, 0, 3), (1, 1, 2), (1+1, 1+2, 2+1)を通る平面と考えることができます.
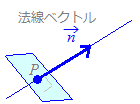
(C) 2つのベクトル=(1,2,1), =(1,1,−1)の両方に垂直なベクトルを求めて,それを平面の法線ベクトルとすることができます.
(A)
点(0, 0, 3)を通り,2つのベクトル=(1,2,1), =(1,1,−1)を含む平面と考えると,2つの媒介変数s, tを用いて
(x,y,z)=(0,0,3)+s(1,1,−1)+t(1,2,1)
と書けるから
 |
x=s+t…(1)
y=s+2t…(2)
z=3−s+t…(3) |
で表される平面を求めればよい.
(1)よりs=x−t
これを(2)(3)に代入
y=(x−t)+2t=x+t…(2’)
z=3−(x−t)+t=3−x+2t…(3’)
次に(2’)×2−(3’)によりtを消去すると
2y−z=2x−3+x
3x−2y+z−3=0
|
 (B)
(B)
3点(0, 0, 3), (1, 1, 2), (2, 3, 3)を通る平面の方程式をax+by+cz+d=0とおくと
 |
3c+d=0…(1)
a+b+2c+d=0…(2)
2a+3b+3c+d=0…(3) |
この連立方程式は不定解をもつから,dを媒介変数として他の文字について解くことにすると
 |
3c=(−d)…(1’)
a+b+2c=(−d)…(2’)
2a+3b+3c=(−d)…(3’) |
(1’)によりc=−d
これを(2’)(3’)に代入してa,bについても解くと
a=−d, b=d
以上により,平面の方程式は
(−d)x+(d)y+(−d)z+(d)=0
3x−2y+z−3=0
(C)
2つのベクトル=(1,2,1), =(1,1,−1)の両方に垂直なベクトル=(3,−2,1)を求めると,平面の方程式は
3x−2y+z−3=0となることがわかります.
|
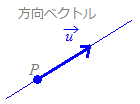
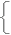
 直線上の点は,方向ベクトルの何倍を足すかを表す媒介変数
直線上の点は,方向ベクトルの何倍を足すかを表す媒介変数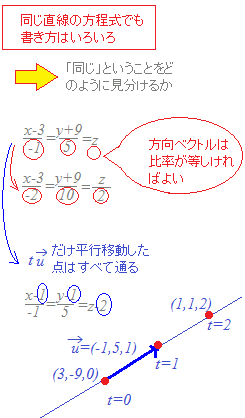
 ≪解説≫
≪解説≫