|
■三角関数の定積分（絶対値付き）
【基本の公式】
（解説）sinx dx=1…(1) sinx dx=2…(2) sinx dx=0…(3) sinnx dx=0 (n=1,2,3,...)…(4)
図で示せば：
(1)←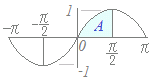 Aの部分の面積が1 計算で示せば： sinx dx=−cosx =(−0)−(−1)=1
図で示せば：
(2)←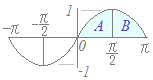 AとBの面積は等しいから合計は2 計算で示せば： sinx dx=−cosx ={−(−1) }−(−1)=2
図で示せば：
(3)←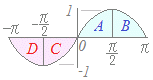 A,B,C,Dの面積は等しいが，符号が逆になっておりC=D=−A=−Bだから，これらを単純に足せば0になる 計算で示せば： sinx dx=−cosx ={−(−1) }−{−(−1) }=0 右に続く→ |
(4)← はじめに，y=sinnxのグラフはy=sinxのグラフを横方向にn倍に引き延ばしたものではなく，n分の１に縮めたものになることに注意しましょう．
この点について，高校生には思い違いが多いので，詳しく述べると
(4)式に戻ると，−π≦x≦πの区間にn=2の場合は，山と谷が２つずつでき，n=3の場合は，山と谷が３つずつできるので，定積分の値は0になります．一般に，y=sinnxとなっているときも同様です．
x=のときsinx=1で山に達しますが x=のとき2x= , sin2x=1となって山に達します さらに x=のとき3x= , sin3x=1となって山に達します  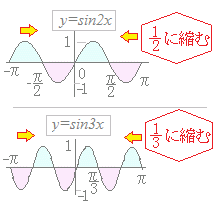 計算で示せば： sinnx dx=−
nが偶数のとき：(−)−(−)=0
となって，いずれの場合も０になります．
nが奇数のとき：()−()=0 |
|
【基本の公式】
（解説）cosx dx=1…(5) cosx dx=0…(6) cosx dx=0…(7) cosnx dx=0 (n=1,2,3,...)…(8)
図で示せば：
(1)←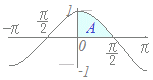 Aの部分の面積が1 計算で示せば： cosx dx=sinx =(1)−(0)=1
図で示せば：
(2)←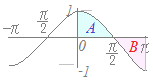 B=−Aだから和は0 計算で示せば： cosx dx=sinx =(0)−(0)=0 右に続く→ |
図で示せば：
(3)←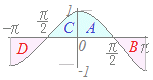 B=D=−A=−Cだから，これらを単純に足せば0になる 計算で示せば： cosx dx=sinx =(0)−(0)=0 (4)← 図で示せば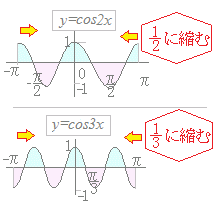 
一般に，y=cosnxとなっている場合には，nxという角度がn倍速く進むので，y=cosxのグラフを横にn分の1に縮めたものになります．
計算で示せば：
cosnx dx==0−0=0 |
|
■絶対値付きの定積分■
【例１】
（解答）|cosx|dxの値を求めてください．
被積分関数に絶対値が付いているときは，区間を場合分けして絶対値記号を外して計算するのが基本です．
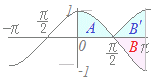0≦x≦→cosx≧0≦x≦π→cosx≦0 だから |cosx|dx=|cosx|dx+|cosx|dx
図のA=1 , B=−1
=cosxdx+(−cosx)dxBの部分を上にひっくり返してB'=1を使うと，A+B'=2になる． =sinx+−sinx =(1−0)+(0−(−1))=2
※高校生のごく初歩的な間違いとして
cosxdxを計算してから絶対値を付けようとする 答案がよくありますが，上記の(6)で示したように，これでは0になって消えてしまいます． ※一般に|f(x)|dx 
と|f(x)dx|は違うので注意 |
【例２】
（解答）|sinx−cosx|dxの値を求めてください．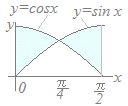 
sin=cos=0≦x≦→cosx≧sinx ≦x≦→cosx≦sinx |sinx−cosx|dx = (cosx−sinx)dx+ (sinx−cosx)dx =sinx−cosx+−cosx−sinx =(+)−(1)+{ (−1)−(−−) } =2−2 |
|
【例３】
（解答）|3sinx−4cosx|dxの値を求めてください．
既知の角度を用いてx>, x<
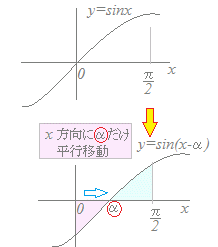
のように書くことができないときでも，その角度を記号定数αなどで表して計算し，結果が出てから戻せばよい．1 ◇三角関数の合成とグラフの平行移動が分かる場合 3sinx−4cosx=(sinx×−cosx×) =5(sinx×−cosx×) と変形する．ここで右図１のような角αを考えると sinα= , cosα= となるから 3sinx−4cosx=5(sinxcosα−cosxsinα) =5sin(x−α) このグラフは，y=5sinxのグラフを右にαだけ平行移動したものだから，右図２（を縦に５倍に引き延ばしたもの）のようになる．
x=α→5sin(x−α)=0
|3sinx−4cosx|dx0≦x≦α→5sin(x−α)≦0 α≦x≦→5sin(x−α)≧0 = |5sin(x−α)|dx =−5 sin(x−α)dx+5 sin(x−α)dx =5cos(x−α)−5cos(x−α) =5{cos0−cos(−α)}−5{cos(−α)−cos0} ここで cos0=1,cos(−α)=cosα=,cos(−α)=sinα= だから （原式）=5{1−}−5{−1}=5−3−4+5=3 右に続く→ |
図１
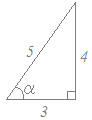  ◇三角関数の合成やグラフの平行移動に自信がない場合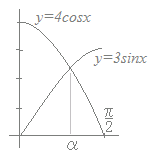 
それぞれ右図のようなグラフになるから交点のx座標をαとおくと 3sinα=4cosαから tanα= 上の図１のような三角形で考えると， sinα= , cosα=
x=α→3sinx=4cosx
（原式）= (−3sinx+4cosx)dx+ (3sinx−4cosx)dx0≦x≦α→3sinx≦4cosx α≦x≦→3sinx≧4cosx =3cosx+4sinx+−3cosx−4sinx ={(3cosα+4sinα)−(3+0)}+{(0−4)−(−3cosα−4sinα)} =6cosα+8sinα−7=6×+8×−7=3 |
|
次の定積分の値を求めてください．
※正しい選択肢の番号をクリックしてください．
なお，暗算ではできませんので，別途計算用紙と筆記用具が必要です． |
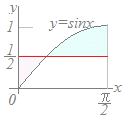x=→sinx=0≦x≦→sinx≦ ≦x≦→sinx≧ だからsinxとは右図のような上下関係になる． |sinx−|dx = (−sinx)dx+ (sinx−)dx =x+cosx+−cosx−x
={(+)−(0+1)}+{(−0−)−(−−)}
=−−1 → 3 |
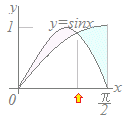y=sinxとy=sin2xの概形は右図のようになるので，交点を求めて上下関係を調べる．sinx=sin2x→sinx=2sinxcosx sinx(2cosx−1)=0 cosx=→x=（矢印の場所） 0≦x≦→sinx≦sin2x ≦x≦→sinx≧sin2x だから |sinx−sin2x|dx = (sin2x−sinx)dx+ (sinx−sin2x)dx =−cos2x+cosx+−cosx+cos2x
= → 1
|
|
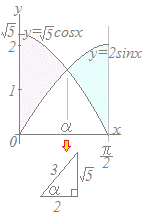y=2sinxとy=cosxの概形は右図のようになるので，交点を求めて上下関係を調べる．2sinx=cosx→tanx= (tanα=,cosα=,sinα=) 0≦x≦α→2sinx≦cosx α≦x≦→2sinx≧cosx だから |2sinx−cosx|dx = (cosx−2sinx)dx+ (2sinx−cosx)dx =sinx+2cosx+−2cosx−sinx ={(sinα+2cosα)−(0+2)} +{(−0−)−(−2cosα−sinα)} =2sinα+4cosα−2−
=2×+4×−2−
=4− → 4 |
|
次のプログラムは，台形公式を使った数値積分によって，コンピュータを使って定積分の値を計算するものです. 結果は小数第4位までの近似値で示されますが，各自の解答と近い値になれば，よい裏付けと見なせます．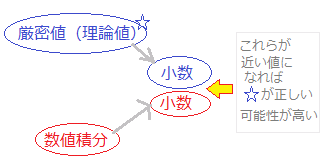 
≪付録１≫
|asinx−bcosx|dx の値を計算します．a, b (≠0)の値を入力して，［計算する］ボタンを押してください． （分数は 1/3, -2/3のように記入．平方根の場合は，例えば，なら2.236のように近似値で記入）
≪付録２≫
|asinx−bcosx|dx の値を計算します．（使用方法は１と同様） |
≪付録３≫
|asinmx+bcosnx|dx の値を計算します．（使用方法は１と同様）
≪付録４≫
|asinmx+bsinnx|dx の値を計算します．（使用方法は１と同様）
≪付録５≫
|acosmx+bcosnx|dx の値を計算します．（使用方法は１と同様） |
...メニューに戻る