|
♪♥♫♦∀== 難易などの目安 ==∳♣♬∅♠
《考え方》 基本★,普通★★,難しい★★★ 《計算量》 少ない☆,普通☆☆,多い☆☆☆ 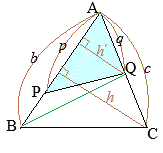 【三角形の面積比】
【三角形の面積比】右図において,△APQの面積は \(\displaystyle\triangle APQ=\triangle ABC\times\frac{p}{b}\times\frac{q}{c}\) に等しい (証明) △ABCと△ABQとは,底辺△ABが共通だから,面積の比は,高さ\(h:h_1\)の比に等しい。 ここで,相似図形の性質により,\(h:h_1=c:q\)だから \(\displaystyle\triangle ABQ=\triangle ABC\times\frac{q}{c}\) 次に,△ABQと△APQとは,高さ\(h_1\)が共通で,面積の比は,底辺の長さ\(b:p\)の比に等しい。 \(\displaystyle\triangle APQ=\triangle ABQ\times\frac{p}{b}\) したがって \(\displaystyle\triangle APQ=\triangle ABC\times\frac{q}{c}\times\frac{p}{b}\)…(証明終)∎
【正四面体(正三角錘)の高さ\(h\),体積\(V\)】
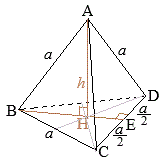 1辺の長さが\(a\) (cm)の正四面体(正三角錐)の高さ\(h\) (cm)は
1辺の長さが\(a\) (cm)の正四面体(正三角錐)の高さ\(h\) (cm)は\(\displaystyle h=\frac{\sqrt{6}}{3}a\) (cm) 1辺の長さが\(a\) (cm)の正四面体(正三角錐)の体積\(V\) (cm3)は \(\displaystyle V=\frac{\sqrt{2}}{12}a\) (cm3) (証明) △BCDは正三角形で,CDの中点をEとおくと \(\displaystyle BC=a, CE=\frac{1}{2}a,BE=\frac{\sqrt{3}}{2}a\) Aから底面△BCDに引いた垂線の足をHとくと,Hは△BCDの重心になっているから \(\displaystyle BH=\frac{2}{3}BE=\frac{\sqrt{3}}{3}a\) △ABHは∠H=90°の直角三角形だから,三平方の定理により \(\displaystyle h^2+\Big(\frac{\sqrt{3}}{3}a\Big)^2=a^2\) \(\displaystyle h^2=a^2-\frac{1}{3}a^2=\frac{2}{3}a^2\) \(\displaystyle h=\sqrt{\frac{2}{3}}a=\frac{\sqrt{6}}{3}a\) (cm)…∎ 次に,体積を(底面積)×(高さ)÷3によって求めると \(\displaystyle V=(a\times\frac{\sqrt{3}}{2}a\div 2)\times\frac{\sqrt{6}}{3}a\div 3=\frac{\sqrt{2}}{12}a^3\) (cm3)…∎ |
【三角錘の体積比】
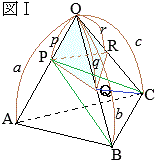 右図Ⅰのような三角錐において,三角錐O-ABCと三角錐O-PQRの体積比 \(V:V'\) は
右図Ⅰのような三角錐において,三角錐O-ABCと三角錐O-PQRの体積比 \(V:V'\) は\(\displaystyle V:V'=abc:pqr\) すなわち \(\displaystyle V'=V\times\frac{p}{a}\times\frac{q}{b}\times\frac{r}{c}\) (証明) 三角錐O-ABCと三角錐O-PBCについて,底面△OBCは共通で高さはa:pだから,その体積比 \(V:V_1\) はa:p \(\displaystyle V_1=V\times\frac{p}{a}\) 三角錐O-PBCと三角錐O-PQCについて,底面△OPCは共通で高さはb:qだから,その体積比 \(V_1:V_2\) はb:q \(\displaystyle V_2=V_1\times\frac{q}{b}\) 三角錐O-PQCと三角錐O-PQRについて,底面△OQCは共通で高さはc:rだから,その体積比 \(V_2:V'\) はc:r \(\displaystyle V'=V_2\times\frac{r}{c}\) したがって \(\displaystyle V'=V\times\frac{p}{a}\times\frac{q}{b}\times\frac{r}{c}\) 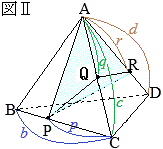 右図Ⅱのような三角錐において,三角錐A-BCDと三角錐A-PQRの体積比 \(V:V'\) は
右図Ⅱのような三角錐において,三角錐A-BCDと三角錐A-PQRの体積比 \(V:V'\) は\(\displaystyle V:V'=bcd:pqr\) すなわち \(\displaystyle V'=V\times\frac{p}{b}\times\frac{q}{c}\times\frac{r}{d}\) (証明) 三角錐A-BCDと三角錐A-PCDについて,底面△ACDは共通で高さはb:pだから,その体積比 \(V:V_1\) はb:p \(\displaystyle V_1=V\times\frac{p}{b}\) 三角錐A-PCDと三角錐A-PQDについて,底面△APDは共通で高さはc:qだから,その体積比 \(V_2:V_2\) はc:q \(\displaystyle V_2=V_1\times\frac{q}{c}\) 三角錐A-PQDと三角錐A-PQRについて,底面△APQは共通で高さはd:rだから,その体積比 \(V_2:V'\) はd:r \(\displaystyle V'=V_2\times\frac{r}{d}\) したがって \(\displaystyle V'=V\times\frac{p}{b}\times\frac{q}{c}\times\frac{r}{d}\) |
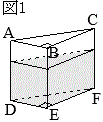
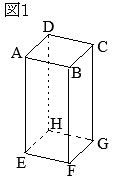
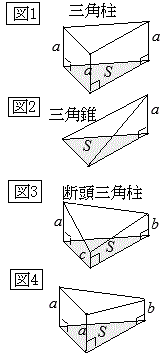 右図1のような底面積が\(S\)で高さが\(h\)の三角柱の体積は
右図1のような底面積が\(S\)で高さが\(h\)の三角柱の体積は フランス革命で断頭台に消えたマリーアントワネットの話は有名
フランス革命で断頭台に消えたマリーアントワネットの話は有名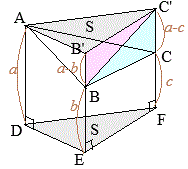 (証明)
(証明)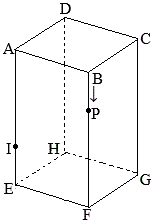
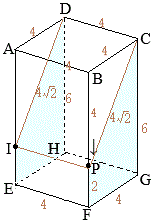 (3) 体積が大きい方の立体は,右図の
(3) 体積が大きい方の立体は,右図の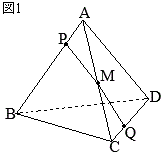
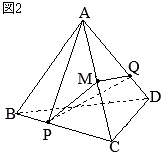 [問2] 次の
[問2] 次の 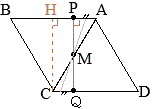 [問1]
[問1]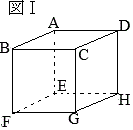
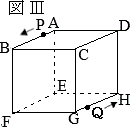
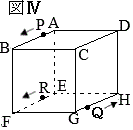
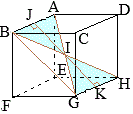 3 線分
3 線分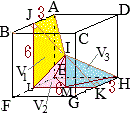 4 図形を見やすくするために,
4 図形を見やすくするために,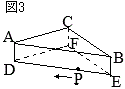
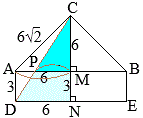 (3)
(3) 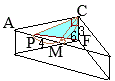
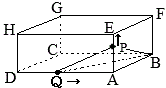
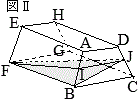
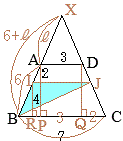
 この容器を,
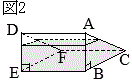
この容器を,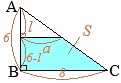 図2において,
図2において,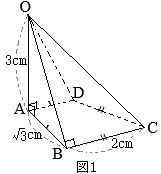
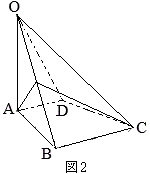 問4 右の図2のように,図1の
四角すい
問4 右の図2のように,図1の
四角すい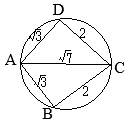 問2
問2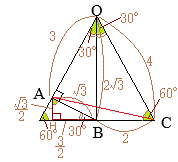 問4
問4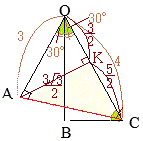 (別解)
(別解)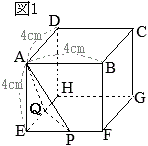
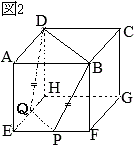 問2 図2において,線分
問2 図2において,線分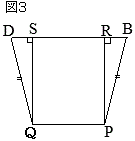 それぞれ
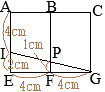
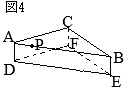
それぞれ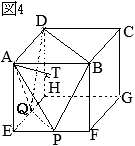 問4 図4のように,点
問4 図4のように,点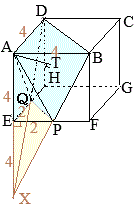 右図のように
右図のように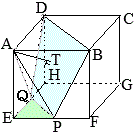
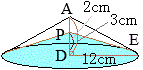
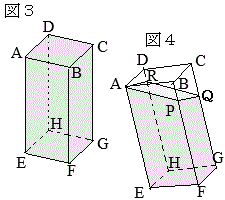 はじめに入っていた水の体積の\(\displaystyle\frac{4}{5}\)倍になるとき,線分
はじめに入っていた水の体積の\(\displaystyle\frac{4}{5}\)倍になるとき,線分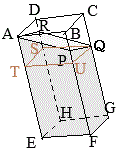 右図のように,
右図のように,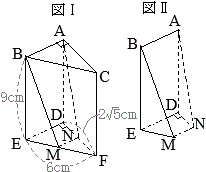
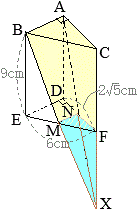 ==
==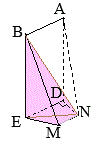 右図のように平面
右図のように平面