2つの三角形が相似であることを証明する方法は3通りある。
- 3組の辺の比が全て等しい
- 2組の辺の比が等しく,その間の角が等しい
- 2組の角がそれぞれ等しい
⇒辺の長さが書いてなければ,「2組の角」で示す
 ★, ☆
★, ☆
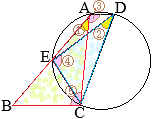
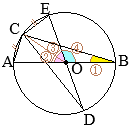
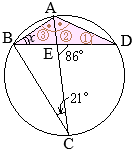
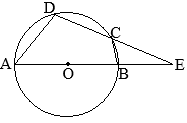
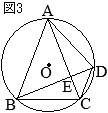
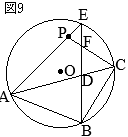
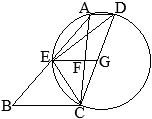
(1)
△ABCと
△DCEについて
- ①=②(弧\(\stackrel{\huge\frown}{\mathrm{EC}}\)の円周角)
- ⑤=③(弧\(\stackrel{\huge\frown}{\mathrm{DC}}\)の円周角)
③=④(平行線の錯角)
ゆえに,④=⑤
以上から,2つの三角形「
△ABCと
△DCEについて」2組の角がそれぞれ等しいから,これらは相似である…(証明終)
★★★, ☆☆☆
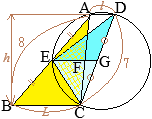
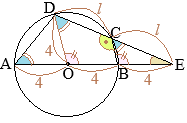
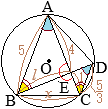
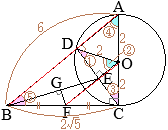
(2)
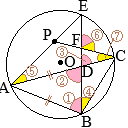
ア
• (1)の結果から,
△ABC∽△DCEで、辺
ABと
DCが対応する
AB:DC=8:7だから,
△ABCと
△DCEの面積比は
\(8^2:7^2=64:49\)
•
AD∥EG∥BCで,
AE=EBだから,
DG=GC
面積比は
△DEG=△CEG
したがって
△ABC:△DEG=64:24.5=128:49
S:△DEG=128:49
\(\displaystyle{\rm \triangle DEG}=\frac{49}{128}S\)…(答)
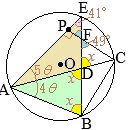
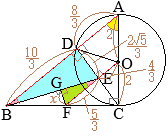
イ
AD=l, BC=Lとおき,
ADから
BCまでの距離を
hとおいて,上記の結果を表す
• \(\displaystyle S=\frac{Lh}{2}\)…(#1)
• \(\displaystyle{\rm EF=\frac{L}{2},FG=\frac{l}{2}}\)
\(\displaystyle{\rm EG=\frac{L}{2}+\frac{l}{2}=\frac{L+l}{2}}\)
\(\displaystyle{\rm \triangle DEG}=\frac{L+l}{2}\times\frac{h}{2}\div 2\)…(#2)

この問題を,時間内に解ける中学生は,エライ!
•(#1)(#2)より
\(\displaystyle\frac{L+l}{2}\times\frac{h}{2}\div 2=\frac{49}{128}\times\frac{Lh}{2}\)
\(\displaystyle\frac{L+l}{4}=\frac{49}{128}\times L\)
\(\displaystyle 128(L+l)=4\times 49L=196L\)
\(\displaystyle 128l=68L\)
\(\displaystyle L=\frac{128}{68}l=\frac{32}{17}l\)
\({\rm AD:BC}=l:L=17:32\)…(答)
→解説を隠す←
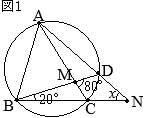
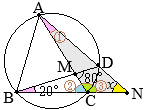
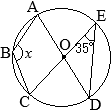
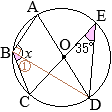
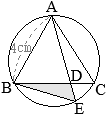
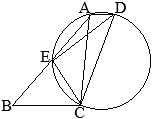
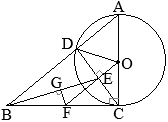
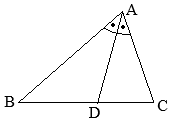 △ABCにおいて,∠Aの二等分線と辺BCとの交点をDとすると
△ABCにおいて,∠Aの二等分線と辺BCとの交点をDとすると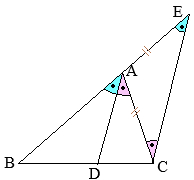 (証明)
(証明)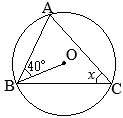
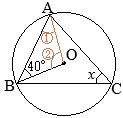 (考え方1)
(考え方1)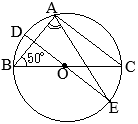
 •
•
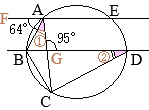

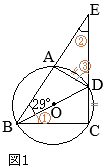 (考え方1)
(考え方1)
 (考え方1)
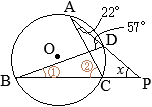
(考え方1)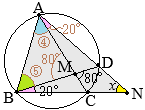 •右の図で
•右の図で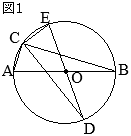
 (考え方1)
(考え方1) (考え方2)
(考え方2)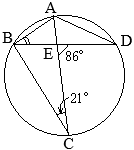
 (考え方1)
(考え方1)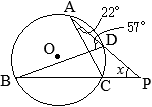
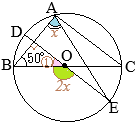
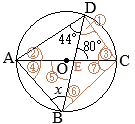
 •同一の弧\(\stackrel{\huge\frown}{\mathrm{DC}}\)の円周角,
•同一の弧\(\stackrel{\huge\frown}{\mathrm{DC}}\)の円周角, (別解裏技1):生徒に教えても委員会??
(別解裏技1):生徒に教えても委員会??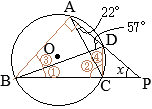 ①=22°
①=22°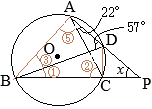 ①=22°
①=22°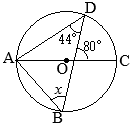
 (考え方1)
(考え方1)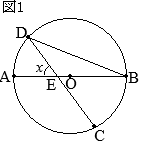
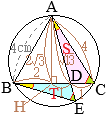
 以上により,2組の角がそれぞれ等しいから
以上により,2組の角がそれぞれ等しいから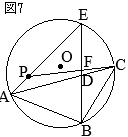
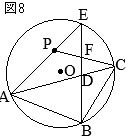
 •
• •
•

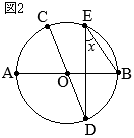
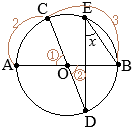
 (2)
(2)
 (1)
(1)  ②
②