|
♪♥♫♦∀== 難易などの目安 ==∳♣♬∅♠
《考え方》 基本★,普通★★,難しい★★★ 《計算量》 少ない☆,普通☆☆,多い☆☆☆
◆三角形の角の二等分線と比◆
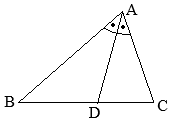 △ABCにおいて,∠Aの二等分線と辺BCとの交点をDとすると
△ABCにおいて,∠Aの二等分線と辺BCとの交点をDとするとAB:AC=BD:DC が成り立つ。
初めて聞いた人は,DがBCの中点になるのかと思うかもしれませんが,そうはなりません。この定理の通り,AB:ACの比に分けられます。
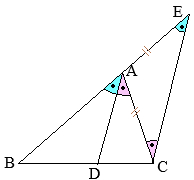 (証明)
(証明)CからADに平行な直線をひき,ABの延長線との交点をEとおくと ∠BAD=∠CAD(仮定) ∠BAD=∠AEC(同位角) ∠CAD=∠ACE(錯角) したがって ∠AEC=∠ACE 2つの角度が等しいから,△ACEは二等辺三角形になり, AE=AC ゆえに AB:AC=AB:AE=BD:DC(平行線と比例の関係) |
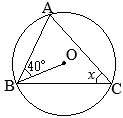 【問題1】
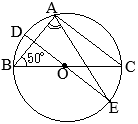
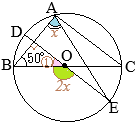
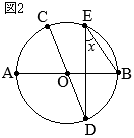
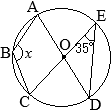
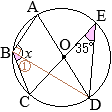
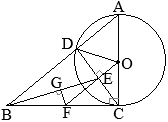
【問題1】右の図のように,円Oの円周上に3つの点A, B, Cがある。∠ABO=40°であるとき,∠xの大きさを答えなさい。 (2025年度 新潟県公立高校入試問題)
※以下の説明では,「見やすく」「分かりやすく」するために,①②・・・などと書いているが,記述式の答案にするときは,それぞれ,∠OAB,∠AOBなどと書く方がよい.
ただし,以下に登場する多くの問題は,「問1小問セット」などの問題で,途中経過不要の穴埋め問題が中心なので,下書きは自分が見やすければよい. ※他の問題も同様
「Oが円の中心」という条件をどう使うか
⇒ OA=OB(=半径)が言える ⇒ ∠AOB=2∠ACB(中心角と円周角の関係)が言える 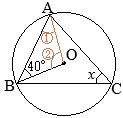 (考え方1)
(考え方1)
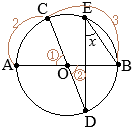
①が分かる→②が分かる→xが分かる
•Oが円の中心だから,OA=OB(=半径)①=40° •△OABの内角の和は180°だから ①+②+40°=180° ②=100° •弧 \(\stackrel{\huge\frown}{\mathrm{AB}}\)の中心角が②だから,円周角∠xは,その半分 ∠x=50°…(答) |
 •
•
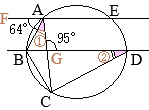

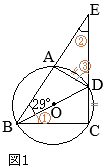 (考え方1)
(考え方1)
 (考え方1)
(考え方1)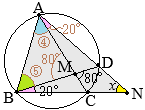 •右の図で
•右の図で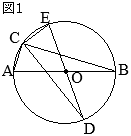
 (考え方1)
(考え方1) (考え方2)
(考え方2)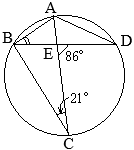
 (考え方1)
(考え方1)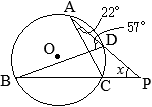
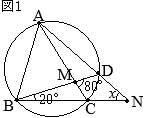
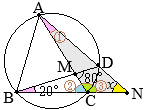
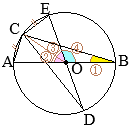
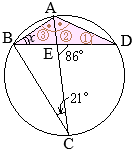
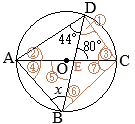
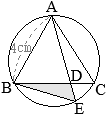
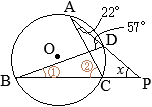 •同一の弧\(\stackrel{\huge\frown}{\mathrm{DC}}\)の円周角,
•同一の弧\(\stackrel{\huge\frown}{\mathrm{DC}}\)の円周角, (別解裏技1):生徒に教えても委員会??
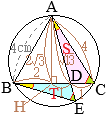
(別解裏技1):生徒に教えても委員会??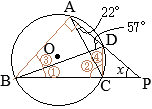 ①=22°
①=22°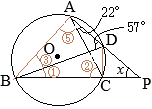 ①=22°
①=22°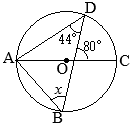
 (考え方1)
(考え方1)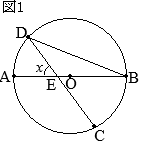
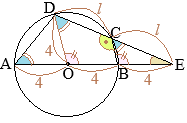
 以上により,2組の角がそれぞれ等しいから
以上により,2組の角がそれぞれ等しいから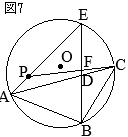
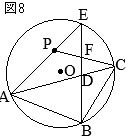
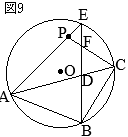
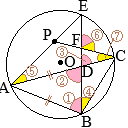 •
•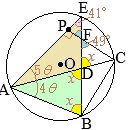 •
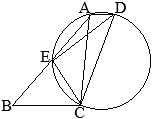
•
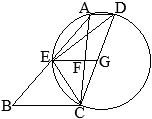
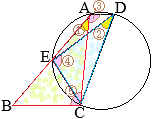
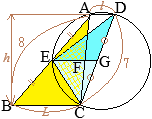 (2)
(2)
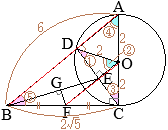 (1)
(1) 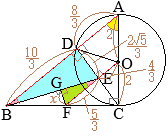 ②
②