�i�j
��, ��
(1)�@
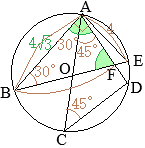
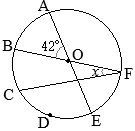
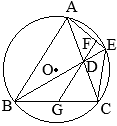
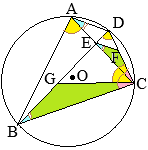
BE�͉~
O�̒��a�ł��邩��C
��EAB=90��
�@����ɁC
��ABE=30���ł��邩��C
��BEA=60��
�@���������āC\({\rm AB=4\sqrt{3}(cm),}\)
���a�́C\(\hspace{2px}{\rm BE=8\hspace{2px}(cm)}\)…�i���j
����, ����
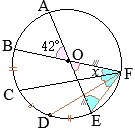
(2)�@
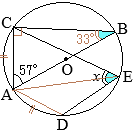
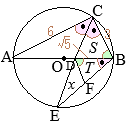
OA=OB�i���a�j������C
��OAB�͓ӎO�p�`�ŁC
��OBA=��OAB=30��
�܂��C
��ACD=45��������C
��CAD=45��
����ɁC
��BAF=75���C
��BFA=180��−(75��+30��)=75��
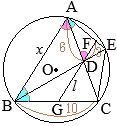
���������āC\({\rm BF=BA=4\sqrt{3}}\)
\({\rm EF=8-4\sqrt{3}}\hspace{2px}(cm)\)…�i���j
 ������, ������
(3)
������, ������
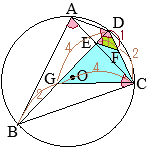
(3)�@�E�}��
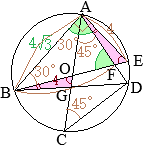
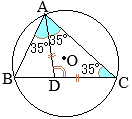
��OBG, ��EAF�ɂ���
- AE=BO=4 (cm)
- ��AEF=60��
��BOG=2��BAO=60��
- ��EAF=��OBG�i�� \(\stackrel{\huge\frown}{\mathrm{ED}}\) �̏�ɗ��~���p�j
😢🥲
��߂��āC�����ł��I
��p�Ƃ��̊Ԃ̕ӂ����ꂼ�ꓙ��������C
��OBG����EAF
�����ŁC
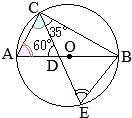
��EAF�̖ʐ�\(S\)�����߂�
(2)�̌��ʂ���C\({\rm EF=8-4\sqrt{3}}\hspace{2px}(cm)\)
���O�p�`
��OEA�̍����́C\(2\sqrt{3}\hspace{2px}(cm)\)
\(\displaystyle S=\frac{(8-4\sqrt{3})\times 2\sqrt{3}}{2}=8\sqrt{3}-12\hspace{2px}(cm^2)\)…�i���j
��������B����
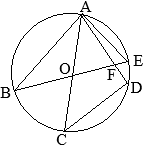
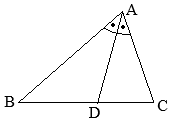 �@��ABC�ɂ����āC��A�̓����ƕ�BC�Ƃ̌�_��D�Ƃ����
�@��ABC�ɂ����āC��A�̓����ƕ�BC�Ƃ̌�_��D�Ƃ����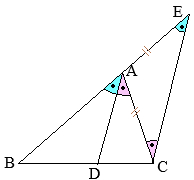 �i�ؖ��j
�i�ؖ��j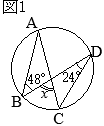
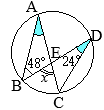 �i�j
�i�j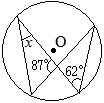
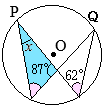 �i�j
�i�j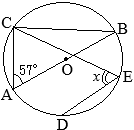
 �i�j
�i�j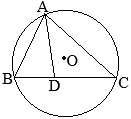
 �@
�@
 �i�l�����P�j�F���S�p
�i�l�����P�j�F���S�p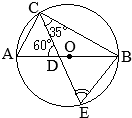
 �@
�@
 (1)�@
(1)�@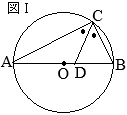

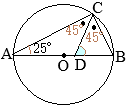
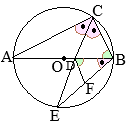
 (1)�@
(1)�@
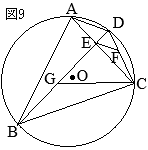

 �ȂǁC�u�h��G�Ō��₷������v�̂����E��
�ȂǁC�u�h��G�Ō��₷������v�̂����E��