仧墌廃妏仧妏偺擇摍暘慄仧
 亂栤戣7亃
亂栤戣7亃
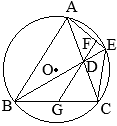
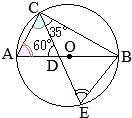
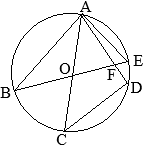
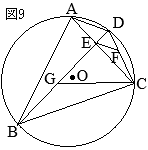
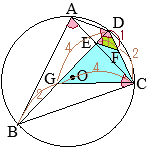
丂塃偺恾偺傛偆偵丆墌 O偺墌廃忋偵3揰 A, B, C傪偲傝丆 仮ABC傪偮偔傞丅
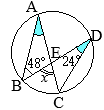
丂 佢ABC偺擇摍暘慄偲慄暘 AC丆墌 O偲偺岎揰傪偦傟偧傟 D, E偲偟丆慄暘 AE傪傂偔丅揰 D傪捠傝慄暘 AB偲暯峴側捈慄偲慄暘 AE, BC偲偺岎揰傪偦傟偧傟 F, G偲偡傞丅
丂偙偺偲偒丆偁偲偺奺栤偄偵摎偊側偝偄丅
丂偨偩偟丆揰 E偼揰 B偲堎側傞揰偲偡傞丅
(1)丂 仮ABD佷仮DAF偱偁傞偙偲傪徹柧偟側偝偄丅
(2)丂 AD=6 cm, DF=3 cm, BC=10 cm偺偲偒丆師偺奺栤偄偵摎偊側偝偄丅
嘆丂慄暘 AB偺挿偝傪媮傔側偝偄丅
嘇丂慄暘 DG偺挿偝傪媮傔側偝偄丅
(2023擭搙 嶰廳導岞棫崅峑擖帋栤戣)
夝愢傪撉傓
乮夝摎乯
仛仛, 仚仚
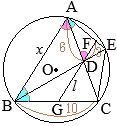
(1)丂 仮ABD偲 仮DAF偵偮偄偰
- AB∥FD偩偐傜嶖妏佢ADF偲佢DAB偼摍偟偄
- 屖 \(\stackrel{\huge\frown}{\mathrm{CE}}\) 偺忋偵棫偮墌廃妏偼摍偟偄偐傜
佢EAC=佢EBC
傑偨丆BE偼佢ABC偺擇摍暘慄偩偐傜佢ABD=佢EBC
偟偨偑偭偰丆佢EAD=佢ABD
2偮偺嶰妏宍偱丆2慻偺妏偑偦傟偧傟摍偟偄偐傜丆 仮ABD佷仮DAF…乮徹柧廔乯
(2)
嘆丂(1)偺寢壥偐傜 AB=x偲偍偔偲
x:AD=AD:DF
x:6=6:3
3x=36
x=12 (cm)…乮摎乯
嘇丂 BE偼 佢ABC偺擇摍暘慄偩偐傜 AB:BC=AD:DC
12:10=6:DC
12DC=60
DC=5
師偵丆 AB∥FD偩偐傜 DG=l偲偍偔偲 AB:AC=l:DC
12:(6+5)=l:5
11l=60
\(\displaystyle l=\frac{60}{11}\hspace{5px}(cm)\)…乮摎乯
仺夝愢傪塀偡仼
|
仧墌廃妏仧妏偺擇摍暘慄仧柺愊斾仧
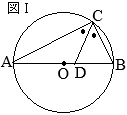 亂栤戣8亃
亂栤戣8亃
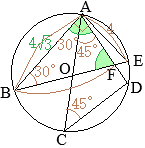
丂 恾嘥偺傛偆偵丆慄暘 AB傪捈宎偲偡傞墌 O偺墌廃忋偵揰 C傪偲傝丆 仮ABC傪偮偔傞丅 佢C偺擇摍暘慄偲曈 AB偲偺岎揰傪 D偲偡傞丅
丂偙偺偲偒丆師偺1, 2偺栤偄偵摎偊側偝偄丅
1丂 佢CAB=25亱偺偲偒丆 佢CDB偺戝偒偝傪媮傔側偝偄丅
 2
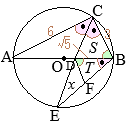
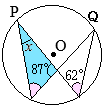
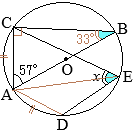
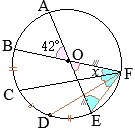
2丂 恾嘦偼丆 恾嘥偵偍偄偰丆慄暘 CD傪墑挿偟偨捈慄偲墌 O偲偺岎揰傪 E偲偟丆慄暘 BE忋偵 CB∥DF偲側傞揰 F傪偲偭偨傕偺偱偁傞丅
丂 AC=6 cm, BC=3 cm偲偡傞偲偒丆師偺(1)乣(3)偺栤偄偵摎偊側偝偄丅
(1)丂 仮BCD佷仮DBF偱偁傞偙偲傪徹柧偟側偝偄丅
(2)丂慄暘 DB偺挿偝傪媮傔側偝偄丅
(3)丂 仮DEF偺柺愊傪媮傔側偝偄丅
(2023擭搙 媨嶈導岞棫崅峑擖帋栤戣)
夝愢傪撉傓
乮夝摎乯
仛, 仚
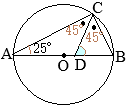 1
1丂 AB偼捈宎偩偐傜丆 佢C=90亱
丂 CD偼 佢C偺擇摍暘慄偩偐傜丆 佢DCA=45亱
丂乽嶰妏宍偺侾偮偺奜妏偼丆偦傟偲椬傝崌傢側偄2偮偺撪妏偺榓偵摍偟偄乿偐傜
丂 佢CDB=佢CAD+佢DCA=25亱+45亱=70亱…乮摎乯
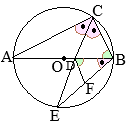 2
仛, 仚
2
仛, 仚
(1)丂 仮BCD偲 仮DBF偵偮偄偰
- CB∥DF偩偐傜佢CBD=佢FDB
- 佢BCD=佢ACD乮壖掕偵傛傞乯
佢ACD=佢DBF乮AE偺墌廃妏乯偩偐傜
佢BCD=佢DBF
2慻偺妏偑偦傟偧傟摍偟偄偐傜丆 仮BCD佷仮DBF…乮徹柧廔乯
仛仛, 仚仚
(2)丂 AB偼捈宎偩偐傜丆 佢C=90亱偱丆嶰暯曽偺掕棟偵傛傝
\({\rm AC^2+CB^2=AB^2 }\)
\({\rm 6^2+3^2=AB^2 }\)
\({\rm AB^2}=36+9=45\)
\({\rm AB}=\sqrt{45}=3\sqrt{5}\)
師偵丆 CD偼 佢C偺擇摍暘慄偩偐傜
\({\rm AD:DB=AC:CB}=6:3=2:1\)
\({\rm DB}=\sqrt{5}\)…乮摎乯
 仛仛仛, 仚仚仚
仛仛仛, 仚仚仚
(3)丂 仮DEF, 仮BCD, 仮DBF偺柺愊傪偦傟偧傟 x, S, T偲偍偔偲
\(\displaystyle{\rm \triangle ABC}=\frac{6\times 3}{2}=9\)
\(\displaystyle S={\rm \frac{\triangle ABC}{3}}=3\)
師偵丆\({\rm DF}\)偺挿偝傪媮傔傞
\(\displaystyle {\rm CB:DB=DB:DF}\)
\(\displaystyle {\rm 3:\sqrt{5}=\sqrt{5}:DF}\)
\(\displaystyle {\rm 3DF}=5\)
\(\displaystyle {\rm DF}=\frac{5}{3}\)
偝傜偵丆\(T\)傪媮傔傞
\(\displaystyle S:T=3^2:(\sqrt{5})^2=9:5\)
\(\displaystyle T=\frac{5}{9}S=\frac{5}{3}\)
柺愊斾偼憡帡斾偺2忔斾偩偐傜
\(\displaystyle x:(x+T+S)=(\frac{5}{3})^2:3^2=\frac{25}{9}:9=25:81\)
\(\displaystyle x:(x+\frac{5}{3}+3)=25:81\)
\(\displaystyle 81x=25(x+\frac{14}{3})\)
\(\displaystyle 56x=25\times\frac{14}{3}\)
\(\displaystyle x=\frac{25\times 14}{3\times 56}=\frac{25}{12}\)…乮摎乯
仺夝愢傪塀偡仼
|
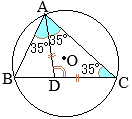
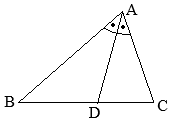 丂仮ABC偵偍偄偰丆佢A偺擇摍暘慄偲曈BC偲偺岎揰傪D偲偡傞偲
丂仮ABC偵偍偄偰丆佢A偺擇摍暘慄偲曈BC偲偺岎揰傪D偲偡傞偲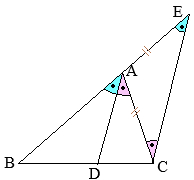 乮徹柧乯
乮徹柧乯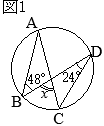
 乮夝摎乯
乮夝摎乯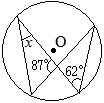
 乮夝摎乯
乮夝摎乯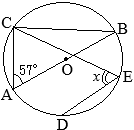
 乮夝摎乯
乮夝摎乯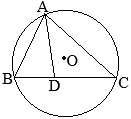
 丂
丂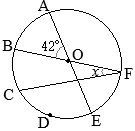
 乮峫偊曽侾乯丗拞怱妏
乮峫偊曽侾乯丗拞怱妏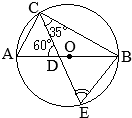
 丂
丂
 (1)丂
(1)丂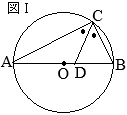

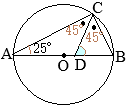
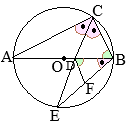

 (1)丂
(1)丂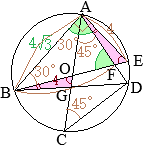
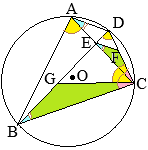

 側偳丆乽揾傝奊偱尒傗偡偔偡傞乿偺傕偍慐傔
側偳丆乽揾傝奊偱尒傗偡偔偡傞乿偺傕偍慐傔