2次関数のグラフと直線とでできる図形の面積
《 解説 》
|
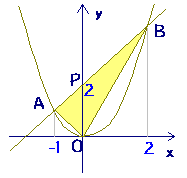
2次関数 y=x2 のグラフと直線 y=x+2 とが交わっているとき,2交点A,Bと原点Oでできる△OABの面積の求め方を考えてみます.
交点A,Bのx座標は
x2=x+2を解いて
(→ x2−x−2=0 → (x+1)(x−2)=0 ) x=−1,2
直線ABがy軸と交わる点Pのy座標は
y=x+2 から y=2
|
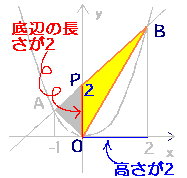
ここで,△OPBの面積は,底辺の長さ2,高さ2と考えると
S1=2×2÷2=2です.
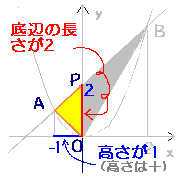
また,△OPAの面積は,底辺の長さ2,高さ1(高さは+にします)と考えると
S2=2×1÷2=1です.
したがって,△OABの面積Sは
S=S1+S2=3 です. |
 |
 |
《 類題 》
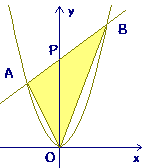 |
2次関数y=x2のグラフと直線y=x+6の交点A,B及び原点Oでできる△OABの面積:
直線ABの切片は 6
A,Bのx座標は x2=x+6 を解いて x=−2,3
S=6×3÷2+6×2÷2=9+6=15・・・(答)
(△OPAの高さは+2です.)
|
《 問題1 》次の空欄を埋めなさい. (タブキーで空欄移動ができます.)
《 問題2 》次の空欄を埋めなさい.
《 問題3 》次の空欄を埋めなさい.
|