�y�ޑ�2.3�z
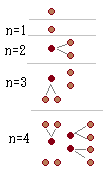
�@A��B�̂Q�l���C�P�̃T�C�R�������̎菇�ɂ�蓊�������D
�@�P��ڂ�A��������D
�@1,2,3�̖ڂ��o����C���̉�ɂ͓����l��������D
�@4,5�̖ڂ��o����C���̉�ɂ͕ʂ̐l��������D
�@6�̖ڂ��o����C�������l�������Ƃ�����ȍ~�͓����Ȃ��D
(1)�@ n��ڂ�A���T�C�R���𓊂���m�� an�����߂�D
(2)�@���傤�� n��ڂ̃T�C�R��������A�����m�� pn�����߂�D
(3)�@ n��ȓ��̃T�C�R��������A�����m�� qn�����߂�D
�i2011�N�x�ꋴ��j
�m������n
(1)�@ n��ڂ�A���T�C�R���𓊂���m���� an�CB��������m���� bn�Ƃ�����
�@ 1��ڂ�A���T�C�R���𓊂���m����
 \( \displaystyle a_1=1 \) \( \displaystyle a_1=1 \)
�@ 1��ڂ�B���T�C�R���𓊂���m����
 \( \displaystyle b_1=0 \) \( \displaystyle b_1=0 \)
�@ 2��ڂ�A���T�C�R���𓊂���̂́C 1��ڂ�A��1,2,3���o���ꍇ������
 \( \displaystyle a_2=\frac{1}{2} \) \( \displaystyle a_2=\frac{1}{2} \)
�@ 2��ڂ�B���T�C�R���𓊂���̂́C 1��ڂ�A��4,5���o���ꍇ������
 \( \displaystyle b_2=\frac{1}{3} \) \( \displaystyle b_2=\frac{1}{3} \)
�@ 3��ڂ�A���T�C�R���𓊂���̂́C�u 2��ڂ�A��������1,2,3���o���ꍇ�v�u 2��ڂ�B��������4,5���o���ꍇ�v������
 \( \displaystyle a_3=a_2\times\frac{1}{2}+ b_2\times\frac{1}{3} \) \( \displaystyle a_3=a_2\times\frac{1}{2}+ b_2\times\frac{1}{3} \)
�@ 3��ڂ�B���T�C�R���𓊂���̂́C�u 2��ڂ�A��������4,5���o���ꍇ�v�u 2��ڂ�B��������1,2,3���o���ꍇ�v������
 \( \displaystyle b_3=a_2\times\frac{1}{3}+ b_2\times\frac{1}{2} \) \( \displaystyle b_3=a_2\times\frac{1}{3}+ b_2\times\frac{1}{2} \)
�@���̘A���Q��������C��ʍ������߂�

 \( \displaystyle a_1=1,\hspace{2px}b_1=0 \) \( \displaystyle a_1=1,\hspace{2px}b_1=0 \)
 \( \displaystyle a_{n+ 1}=a_n\times\frac{1}{2}+ b_n\times\frac{1}{3} \) \( \displaystyle a_{n+ 1}=a_n\times\frac{1}{2}+ b_n\times\frac{1}{3} \)���(*1)
 \( \displaystyle b_{n+1}=a_n\times\frac{1}{3}+ b_n\times\frac{1}{2} \) \( \displaystyle b_{n+1}=a_n\times\frac{1}{3}+ b_n\times\frac{1}{2} \)���(*2)
) \( \displaystyle a_{n+ 1}-\alpha b_{n+ 1}=\beta(a_n-\alpha b_n) \) \( \displaystyle a_{n+ 1}-\alpha b_{n+ 1}=\beta(a_n-\alpha b_n) \)�ƂȂ�  \( \displaystyle \alpha,\hspace{2px}\beta \) \( \displaystyle \alpha,\hspace{2px}\beta \)���W����r�ɂ���ċ��߂��

 \( \displaystyle \frac{1}{2}-\frac{\alpha}{3}=\beta \) \( \displaystyle \frac{1}{2}-\frac{\alpha}{3}=\beta \)���(*3)
 \( \displaystyle \frac{1}{3}-\frac{\alpha}{2}=-\alpha\beta \) \( \displaystyle \frac{1}{3}-\frac{\alpha}{2}=-\alpha\beta \)���(*4)
(*3)(*4)���

 \( \displaystyle \alpha=1,\hspace{2px}\beta=\frac{1}{6} \) \( \displaystyle \alpha=1,\hspace{2px}\beta=\frac{1}{6} \)���(*5)
 \( \displaystyle \alpha=-1,\hspace{2px}\beta=\frac{5}{6} \) \( \displaystyle \alpha=-1,\hspace{2px}\beta=\frac{5}{6} \)���(*6)
(*5)���
) \( \displaystyle a_{n+ 1}-b_{n+ 1}=\frac{1}{6}(a_n-b_n) \) \( \displaystyle a_{n+ 1}-b_{n+ 1}=\frac{1}{6}(a_n-b_n) \)
�@����  \( \displaystyle \{a_n-b_n\} \) \( \displaystyle \{a_n-b_n\} \)�́C����  \( a_1-b_1=1 \) \( a_1-b_1=1 \)�C����  \( \displaystyle \frac{1}{6} \) \( \displaystyle \frac{1}{6} \)�̓��䐔��ɂȂ邩��
^{n-1}) \( \displaystyle a_{n}-b_{n}=(\frac{1}{6})^{n-1} \) \( \displaystyle a_{n}-b_{n}=(\frac{1}{6})^{n-1} \)���(*7)
(*6)���
) \( \displaystyle a_{n+ 1}+ b_{n+ 1}=\frac{5}{6}(a_n+ b_n) \) \( \displaystyle a_{n+ 1}+ b_{n+ 1}=\frac{5}{6}(a_n+ b_n) \)
�@����  \( \displaystyle \{a_n+ b_n\} \) \( \displaystyle \{a_n+ b_n\} \)�́C����  \( \displaystyle a_1+ b_1=1 \) \( \displaystyle a_1+ b_1=1 \)�C����  \( \displaystyle \frac{5}{6} \) \( \displaystyle \frac{5}{6} \)�̓��䐔��ɂȂ邩��
^{n-1}) \( \displaystyle a_{n}+ b_{n}=(\frac{5}{6})^{n-1} \) \( \displaystyle a_{n}+ b_{n}=(\frac{5}{6})^{n-1} \)���(*8)
{(*7)+(*8)}��2�ɂ��
^{n-1}%2B(\frac{1}{6})^{n-1}\}) \( \displaystyle a_{n}=\frac{1}{2}\Big\{(\frac{5}{6})^{n-1}+(\frac{1}{6})^{n-1}\Big\} \) \( \displaystyle a_{n}=\frac{1}{2}\Big\{(\frac{5}{6})^{n-1}+(\frac{1}{6})^{n-1}\Big\} \)
(2)
n��ڂ�A���T�C�R���𓊂��āC6�̖ڂ��o��ꍇ������
^{n-1}%2B(\frac{1}{6})^{n-1}\}) \( \displaystyle p_n=a_{n}\times\frac{1}{6}=\frac{1}{12}\Big\{(\frac{5}{6})^{n-1}+(\frac{1}{6})^{n-1}\Big\} \) \( \displaystyle p_n=a_{n}\times\frac{1}{6}=\frac{1}{12}\Big\{(\frac{5}{6})^{n-1}+(\frac{1}{6})^{n-1}\Big\} \)
(3) n��ŏ��Ƃ����݂̂͌��ɔr�����ۂȂ̂ŁC n��ȉ��ŏ��m���́C�����̘a�ŋ��߂���
^{k-1}%2B\sum_{k=1}^n(\frac{1}{6})^{k-1}\}\]) \( \displaystyle q_n=\sum_{k=1}^n p_k=\frac{1}{12}\{\sum_{k=1}^n(\frac{5}{6})^{k-1}+\sum_{k=1}^n(\frac{1}{6})^{k-1}\} \) \( \displaystyle q_n=\sum_{k=1}^n p_k=\frac{1}{12}\{\sum_{k=1}^n(\frac{5}{6})^{k-1}+\sum_{k=1}^n(\frac{1}{6})^{k-1}\} \)
{�@}���̑�1���́C���� 1�C����  \( \displaystyle \frac{5}{6} \) \( \displaystyle \frac{5}{6} \)�C���� n�̓��䐔��̘a������
^n}{1-\frac{5}{6}}=6\{1-(\frac{5}{6})^n\}) \( \displaystyle \frac{1-(\dfrac{5}{6})^n}{1-\dfrac{5}{6}}=6\Big\{1-(\frac{5}{6})^n\Big\} \) \( \displaystyle \frac{1-(\dfrac{5}{6})^n}{1-\dfrac{5}{6}}=6\Big\{1-(\frac{5}{6})^n\Big\} \)
{�@}���̑�2���́C���� 1�C����  \( \displaystyle \frac{1}{6} \) \( \displaystyle \frac{1}{6} \)�C���� n�̓��䐔��̘a������
^n}{1-\frac{1}{6}}=\frac{6}{5}\{1-(\frac{1}{6})^n\}) \( \displaystyle \frac{1-(\dfrac{1}{6})^n}{1-\dfrac{1}{6}}=\frac{6}{5}\Big\{1-(\frac{1}{6})^n\Big\} \) \( \displaystyle \frac{1-(\dfrac{1}{6})^n}{1-\dfrac{1}{6}}=\frac{6}{5}\Big\{1-(\frac{1}{6})^n\Big\} \)
����
^n\}%2B\frac{1}{10}\{1-(\frac{1}{6})^n\}\]) \( \displaystyle q_n=\frac{1}{2}\Big\{1-(\frac{5}{6})^n\Big\}+\frac{1}{10}\{1-(\frac{1}{6})^n\} \) \( \displaystyle q_n=\frac{1}{2}\Big\{1-(\frac{5}{6})^n\Big\}+\frac{1}{10}\{1-(\frac{1}{6})^n\} \)
^n-\frac{1}{10}(\frac{1}{6})^n) \( \displaystyle =\frac{3}{5}-\frac{1}{2}(\frac{5}{6})^n-\frac{1}{10}(\frac{1}{6})^n \)
�����適 \( \displaystyle =\frac{3}{5}-\frac{1}{2}(\frac{5}{6})^n-\frac{1}{10}(\frac{1}{6})^n \)
�����適
|
 �y�ޑ�2.4�z
�y�ޑ�2.4�z
�@ xy���ʏ�̂U�̓_ (0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)���}�̂悤�ɒ���1�̐����Ō���Ă���D���_ X�́C�����̓_�̏�����̋K���ɏ]���ĂP�b���ƂɈړ�����D
�K���F
���_X�́C���̂Ƃ��Ɉʒu����_����o�钷���P�̐����ɂ���Č����}�̓_�̂����ꂩ�ɁC�������m���ňړ�����D
�@�Ⴆ�C X�� (2, 0)�ɂ���Ƃ��́C (1, 0), (2, 1)�̂����ꂩ��  \( \displaystyle \frac{1}{2} \) \( \displaystyle \frac{1}{2} \)�̊m���ňړ�����D�܂��C X�� (1, 1)�ɂ���Ƃ��́C (0, 1), (1, 0), (2, 1)�̂����ꂩ��  \( \displaystyle \frac{1}{3} \) \( \displaystyle \frac{1}{3} \)�̊m���ňړ�����D
�@���� 0�œ��_ X�� O=(0, 0)����o������Ƃ��C n�b��� X�� x���W�� 0�ł���m�������߂�D�������C n�� 0�ȏ�̐����Ƃ���D
�i2016�N�x���s�嗝�Ȍn�j
�m������n

�@ n�b��� X�� x���W�� 0�ł���F (0, 0)�܂��� (0, 1)�ɂ���m���� pn�C x���W�� 1�ł���F (1, 0)�܂��� (1, 1)�ɂ���m���� qn�C x���W�� 2�ł���F (2, 0)�܂��� (2, 1)�ɂ���m���� rn�ŕ\����
 \( \displaystyle p_0=1,\hspace{2px}q_0=0,\hspace{2px}r_0=0 \) \( \displaystyle p_0=1,\hspace{2px}q_0=0,\hspace{2px}r_0=0 \)
 \( \displaystyle p_1=\frac{1}{2},\hspace{2px}q_1=\frac{1}{2},\hspace{2px}r_1=0 \) \( \displaystyle p_1=\frac{1}{2},\hspace{2px}q_1=\frac{1}{2},\hspace{2px}r_1=0 \)

 \( \displaystyle p_{n+ 1}=p_n\times\frac{1}{2}+ q_n\times\frac{1}{3} \) \( \displaystyle p_{n+ 1}=p_n\times\frac{1}{2}+ q_n\times\frac{1}{3} \)���(*1)
 \( \displaystyle q_{n+1}=p_n\times\frac{1}{2}+ q_n\times\frac{1}{3}+ r_n\times\frac{1}{2} \) \( \displaystyle q_{n+1}=p_n\times\frac{1}{2}+ q_n\times\frac{1}{3}+ r_n\times\frac{1}{2} \)���(*2)
 \( \displaystyle r_{n+ 1}=q_n\times\frac{1}{3}+ r_n\times\frac{1}{2} \) \( \displaystyle r_{n+ 1}=q_n\times\frac{1}{3}+ r_n\times\frac{1}{2} \)���(*3)
�y���Ӂz
�@���̂悤�� �O�d�̘A���Q�������u�L���ʗp�����ʓI�ȉ������ʼn����Ȃ���Ȃ�Ȃ��v�ȂǂƊ�Ȑ��`�������K�v�͂Ȃ��D���������C���Z���w�̋��ȏ��ɂ͘A���Q�����͍ڂ��Ă��炸�i�茳�ɂ���3�Ёj�C�O�d�̘A���ƂȂ�ƁC�قƂ�ǂ̐��k�͉��������Ƃ��Ȃ��D
�@�萔���Ȃ��Œ萔�W���̏ꍇ�͈ꎟ�ϊ��ƌĂ�C�s��ŏ�����
 \( \displaystyle \begin{pmatrix}p_{n+ 1}\\q_{n+ 1}\\ r_{n+ 1}\end{pmatrix}=\begin{pmatrix}a& b& c\\ d& e& f\\ g& h& i\end{pmatrix} \) \( \displaystyle \begin{pmatrix}p_{n+ 1}\\q_{n+ 1}\\ r_{n+ 1}\end{pmatrix}=\begin{pmatrix}a& b& c\\ d& e& f\\ g& h& i\end{pmatrix} \) \( \displaystyle \begin{pmatrix}p_{n}\\q_{n}\\ r_{n}\end{pmatrix} \) \( \displaystyle \begin{pmatrix}p_{n}\\q_{n}\\ r_{n}\end{pmatrix} \)
�̉���
 \( \displaystyle \begin{pmatrix}p_{n}\\q_{n}\\ r_{n}\end{pmatrix}=\begin{pmatrix}a& b& c\\ d& e& f\\ g& h& i\end{pmatrix}^{n-1} \) \( \displaystyle \begin{pmatrix}p_{n}\\q_{n}\\ r_{n}\end{pmatrix}=\begin{pmatrix}a& b& c\\ d& e& f\\ g& h& i\end{pmatrix}^{n-1} \) \( \displaystyle \begin{pmatrix}p_{1}\\q_{1}\\ r_{1}\end{pmatrix} \) \( \displaystyle \begin{pmatrix}p_{1}\\q_{1}\\ r_{1}\end{pmatrix} \)
�Ɖ����邪�C���̊w�K�w���v�̂ł́i2021�N���݁j���Z���w�ɍs��͂Ȃ��C�s��� n����Ȃ��D�s����K���Ă��Ă��C�s��� n�����̓I�ɋ��߂邱�Ƃ́C���ꂾ���ł����̐܂����ɂȂ�D
�@�����ł́u���̖������ԓ��ɉ������@�����R�ɂł�������悢�v�Ɗ���邱�Ƃ��d�v����ȉ��̓��ẮC���܂��܉�������������Ă���
(*1)+(*2)+(*3)���
 \( \displaystyle p_{n+ 1}+ q_{n+ 1}+ r_{n+ 1}=p_n+ q_n+ r_n \) \( \displaystyle p_{n+ 1}+ q_{n+ 1}+ r_{n+ 1}=p_n+ q_n+ r_n \)
����������
 \( \displaystyle p_n+ q_n+ r_n=\cdots=p_0+ q_0+ r_0=1 \) \( \displaystyle p_n+ q_n+ r_n=\cdots=p_0+ q_0+ r_0=1 \)
(*2)�ɑ�������
) \( \displaystyle q_{n+ 1}=p_n\times\frac{1}{2}+ q_n\times\frac{1}{3}+\frac{1}{2}(1-p_n-q_n) \) \( \displaystyle q_{n+ 1}=p_n\times\frac{1}{2}+ q_n\times\frac{1}{3}+\frac{1}{2}(1-p_n-q_n) \)
 \( \displaystyle q_{n+ 1}=-\frac{1}{6}q_n+\frac{1}{2} \) \( \displaystyle q_{n+ 1}=-\frac{1}{6}q_n+\frac{1}{2} \)
) \( \displaystyle q_{n+1}-\frac{3}{7}=-\frac{1}{6}(q_n-\frac{3}{7}) \) \( \displaystyle q_{n+1}-\frac{3}{7}=-\frac{1}{6}(q_n-\frac{3}{7}) \)
(-\frac{1}{6})^{n-1}) \( \displaystyle q_{n}-\frac{3}{7}=(q_1-\frac{3}{7})(-\frac{1}{6})^{n-1} \) \( \displaystyle q_{n}-\frac{3}{7}=(q_1-\frac{3}{7})(-\frac{1}{6})^{n-1} \)
^{n-1}) \( \displaystyle q_{n}=\frac{3}{7}+ \frac{1}{14}(-\frac{1}{6})^{n-1} \) \( \displaystyle q_{n}=\frac{3}{7}+ \frac{1}{14}(-\frac{1}{6})^{n-1} \)���(*4)
�܂��C(*1)−(*3)���
) \( \displaystyle p_{n+ 1}-r_{n+ 1}=\frac{1}{2}(p_n-r_n) \) \( \displaystyle p_{n+ 1}-r_{n+ 1}=\frac{1}{2}(p_n-r_n) \)
(\frac{1}{2})^{n-1}=(\frac{1}{2})^{n}) \( \displaystyle p_{n}-r_{n}=(p_1-r_1)(\frac{1}{2})^{n-1}=(\frac{1}{2})^{n} \) \( \displaystyle p_{n}-r_{n}=(p_1-r_1)(\frac{1}{2})^{n-1}=(\frac{1}{2})^{n} \)���(*5)
(*4)(*5)��(*2)�ɑ������
^{n}=p_n\times\frac{1}{2}%2B\{\frac{3}{7}%2B \frac{1}{14}(-\frac{1}{6})^{n-1}\}\times\frac{1}{3}) \( \displaystyle \frac{3}{7}\!+\! \frac{1}{14}(-\frac{1}{6})^{n}=p_n\times\frac{1}{2}\!+\!\{\frac{3}{7}\!+\! \frac{1}{14}(-\frac{1}{6})^{n-1}\}\times\frac{1}{3} \) \( \displaystyle \frac{3}{7}\!+\! \frac{1}{14}(-\frac{1}{6})^{n}=p_n\times\frac{1}{2}\!+\!\{\frac{3}{7}\!+\! \frac{1}{14}(-\frac{1}{6})^{n-1}\}\times\frac{1}{3} \)
^n)\times\frac{1}{2}) \( \displaystyle +(p_n-(\frac{1}{2})^n)\times\frac{1}{2} \) \( \displaystyle +(p_n-(\frac{1}{2})^n)\times\frac{1}{2} \)
^n%2B\frac{1}{2^{n%2B 1}}) \( \displaystyle p_n=\frac{2}{7}+\frac{3}{14}(-\frac{1}{6})^n+\frac{1}{2^{n+ 1}} \)
�����適 \( \displaystyle p_n=\frac{2}{7}+\frac{3}{14}(-\frac{1}{6})^n+\frac{1}{2^{n+ 1}} \)
�����適
|
 �i�j
�i�j �@
�@ �y�ޑ�2.4�z
�y�ޑ�2.4�z �@
�@