|
(1) 次の方程式を解け．解は１．〜５．から選べ． x−1= １． x=−4 |
【無理方程式】 x−1= ⇔ (x−1)2=13−x かつ x−1≧0 ⇔ x2−x−12=0 かつ x≧1 ⇔ x=4 , −3 かつ x≧1 ⇔ x=4 |
| (2) 次の不等式の解を下の選択肢から選べ． x−4≧ １． −2≦x≦4 |
【無理不等式】 原式 ⇔ (x−4)2≧4(7−x) かつ 7−x≧0 かつ x−4≧0 ⇔ x2−4x−12≧0 かつ 4≦x≦7 
⇔ x≦−2 , 6≦x かつ 4≦x≦7 ⇔ 6≦x≦7 |
| (3) 次の不等式の解を下の選択肢から選べ． x−2≦ １． −2≦x≦2 |
【無理不等式】 （ア） x≧2 のとき (x−2)2≦20−x2 より −2≦x≦4 ゆえに，2≦x≦4 （イ） x<2 のとき 20−x2≧0 より −2≦x≦2 ゆえに，−2≦x<2 （ア）（イ）より，−2≦x≦4 |
| (4) 次の不等式の解を下の選択肢から選べ． −≦ １． x<−1 , 2≦x<3   お疲れさまでした．写真は京都御苑 |
【分数不等式】 （原式） ⇔ ≦ ⇔ ≦0 ⇔ x≠3 ,−1 かつ (x−2)(x−3)(x+1)≦0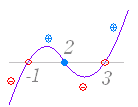 
⇔ x<−1 , 2≦x<3
|