無理方程式，無理不等式，分数方程式，分数不等式

■無理方程式，無理不等式，分数方程式，分数不等式 （高校数学 IIＩ）
　　　　　　　　　　　　※該当する選択肢をクリックせよ．（［採点］は下端でまとめて行う．採点すれば［解説］も出る．全問合えば写真が出る．）（※問題は過去問ではない．）

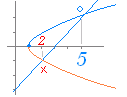
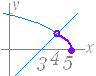
(1)
　次の方程式を解け．解は１．～５．から選べ．

=x−3

１．　x=2
２．　x=5
３．　x=2 , 5
４．　x=−2 , 5
５．　x=2 ,−5

=x−3 ⇔ x−1=(x−3)2 かつ x−3≧0
⇔ x2−7x+10=0 かつ x≧3
⇔ x=2 , 5 かつ x≧3
⇔ x=5

【無理方程式】
=g(x)　…(1)
⇔　f(x)={g(x)}2 …(2)かつ g(x)≧0 …(3)

（公式の解説）
○　(1)の両辺を２乗して根号を取り除くと f(x)={g(x)}2 となるが
g(x)<0 の場合が混入してくるので，g(x)≧0 …(3) を条件に追加しなければならない．
( 数字で確認：9=32 , 9=(−3)2 が成り立つとき
=3 は成り立つが =(−3) は成り立たない．)

○　少し詳しい解説：
　もともと，(1)において根号の中は正（または0）でなければならないから，f(x)≧0　…(A)
　このとき，と等しくなるには g(x)≧0 …(B)
　(A)(B)が成り立つとき，両辺を２乗して f(x)={g(x)}2 …(C) を解けばよい．
すなわち (1) ⇔ (A)(B)(C)
　このままでもよいが，{g(x)}2≧0 だから，(C)が成り立つ解では f(x)≧0 が成り立ち，条件(A)はなくてもよい．
　結局， (1) ⇔ (A)(B)(C) ⇔ (B)(C)
（※　(C)の解のうち(1)に代入して成り立つものを解としてもよい．）

(2)
　次の方程式（ア）～（ウ）の解として正しい組合せを1．～５．から選べ

（ア）　 =x−1　（イ）　 =1−x
（ウ）　 =x+1

１．　（ア）　x=2　，　（イ）　x=−3，　（ウ）　x=1
２．　（ア）　x=−3　，　（イ）　x=2，　（ウ）　x=1
３．　（ア）　x=2　，　（イ）　x=−3，　（ウ）　x=−6
４．　（ア）　x=−3　，　（イ）　x=2，　（ウ）　x=−6
５．　（ア）　x= -3　，　（イ）　x=2，　（ウ）　x=−6 , 1

【無理方程式】
（ア）　7−3x=x2−2x+1 かつ x≧1 ⇔ x2+x−6=0 かつ x≧1 ⇔ x=2
（イ）　7−3x=x2−2x+1 かつ x≦1 ⇔ x2+x−6=0 かつ x≦1 ⇔ x=−3
（ウ）　7−3x=x2+2x+1 かつ x≧−1 ⇔ x2+5x−6=0 かつ x≧−1 ⇔ x=1

(3)
　次の不等式の解を下の選択肢から選べ． < x−3

１．　x<1 , 4<x
２．　x<1 , 4<x≦5
３．　4<x≦5
４．　4≦x<5
５．　4<x<5

< x−3 ⇔ 5−x < (x−3)2 かつ 5−x≧0 かつ x−3>0

⇔ x2−5x+4>0 かつ 3<x≦5
⇔ x<1 , 4<x かつ 3<x≦5
⇔ 4<x≦5

【無理不等式(1)】
< g(x)　…(1)
⇔　f(x)<{g(x)}2 …(2)　かつ　0≦f(x) …(3)　かつ　0<g(x) …(4)

（公式の解説）
○　根号の中にある f(x) は0以上でなければならない …(A)
　また，≧0だから g(x) は正でなければならない …(B)（ g(x)=0 のときは f(x) の取りうる値がない）
　(1)(2)の条件の下に両辺を２乗して，f(x)<{g(x)}2 …(C)
※　無理方程式の場合と異なり，(C)を満たすものの中には f(x)<0 となるものが含まれる場合があるから，(C)は省略できない．
※ ≦g(x)　…(1)　のときは　f(x)≦{g(x)}2 …(2)　かつ　0≦f(x) …(3)　かつ　0≦g(x) …(4) になる．

(4)
　　次の不等式の解を下の選択肢から選べ． > x−1 　

１．　x<4
２．　- 5≦x<4
３．　- 5<x<4
４．　- 3≦x<4
５．　1≦x<4

> x−1
（ア）　x−1≧0　かつ　25−x2 > (x−1)2
⇔ x≧1　かつ　x2 −x−12<0
⇔ x≧1　かつ　- 3 <x<4 ⇔ 1≦x<4
（イ）　x−1<0　かつ　25−x2≧0
⇔ x<1　かつ　- 5≦x≦5 ⇔ - 5≦x<1
（ア）（イ）より - 5≦x<4

【無理不等式(2)】
> g(x)　…(1)
⇔ (　g(x)≧0 …(2)　かつ　f(x)>{g(x)}2 …(3))
または（ g(x)<0 …(4)　かつ　f(x)≧0 …(5) ）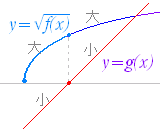

（公式の解説）
　前の場合と異なり，g(x)<0　かつ　f(x)≧0 の場合は，２乗するまでもなく直ちに成立するので，これを追加しなくてはならない．
　g(x) の正負によって分けて考えると分かりやすい．
（ア）　g(x)≧0 のときは２乗比較する（ただし，f(x)>{g(x)}2 を満たすものについては f(x)≧0 は省略できる．）．
（イ）　g(x)<0 のときは f(x)≧0 だけでよい．

(5)
　次の方程式の解を求めよ．

.=2+

１．　x=2
２．　x=−1
３．　x=−2
４．　x=2 ,−1
５．　x=−2 , 1

【分数方程式】
　分数方程式　=0　を解くには，

分子が0となる値のうちで，分母が0とならないものを求めればよい．
　　 f(x)=0 …(1) g(x)≠0 …(2)

（公式の解説）
分数方程式の分母を払うなどの変形を行うと，元の式で分母が0となる値が含まれることがあるが，この値は元の方程式の解ではないので除外する．

x≠2 …(1)
x2+x=2(x−2)+6
x2−x−2=0 ⇔ x=2 ,−1 …(2)
(1)(2)より x=−1

(6)
　次の不等式を解け．

. <

１．　x>4
２．　x<−2 , 1<x≦4
３．　- 2<x<1 , 4≦x
４．　x<−2 , 1<x<4
５．　- 2<x<1 , 4<x

[採点する]

お疲れさまでした．写真は京都御苑

【分数不等式】
　分数不等式　>0 ⇔ f(x)g(x)>0

　分数不等式　≧0 ⇔ f(x)g(x)≧0 かつ g(x)≠0

（公式の解説）
　積と商は値は異なるが符号は一致するので，商の符号は積の符号で調べられる．（「正÷正＝正，正÷負＝負，負÷正＝負，負÷負＝正」の符号は，各々「正×正＝正，正×負＝負，負×正＝負，負×負＝正」の符号と一致する．）これは，分母の２乗 g(x)2≧0 を掛けても符号は変らないと考えてもよい．
　≧0　のときは，分母が0となる値を除外しなければならない．

< ⇔ −<0 ⇔ <0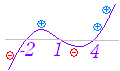

⇔ <0

⇔ >0

⇔ (x−4)(x−1)(x+2)>0⇔ - 2<x<1 , 4<x

○===メニューに戻る