| (1) 65 人の学生に,昨日の食事について,麺類・パン類・ご飯類のどれを食べたか調査したところ,麺類を食べた学生は 28 人,パン類を食べた学生は 31 人,麺類もパン類も食べた学生は 11 人で,3種類のどれも食べなかった学生はいなかった. ご飯類だけを食べた学生は何人か. |
(1)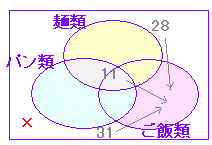 n(A∪B)=n(A)+n(B) - n(A∩B)=28+31 - 11=48 だから, これを全体の人数から引いて 65 - 48 =17 |
| (2) 40 人の学生に,昨日の食事について調査したところ,麺類を食べた学生は 18 人,パン類を食べた学生は 17 人,ご飯類を食べた学生は 16 人で,3種類のどれも食べなかった学生はいなかった. 3種類とも食べた学生数の最大値を求めよ. |
(2)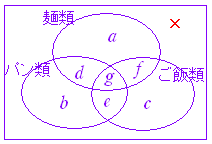
a+b+c+d+e+f+g=40 …(2) だから (1)-(2) により d+e+f+2g=11 …(3) ただし 0≦d , e , f , g …(4) (3)(4)より g≦5 |
| (3) 1 から 1000 までの整数のうち 2 , 3 , 5 のうち2つ以上で割り切れるものは何個あるか.ただし,10 の倍数は除く. |
(3)
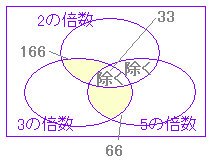
○ 15 の倍数は,1000÷15=66 … 10 により 66 個 ○ 30 の倍数は,1000÷30=33 … 10 により 33 個 166+66 - 2×33=166 |
| (4) 3 桁の正の整数で 3 でも 5 でも 7 でも割り切れないものは何個あるか.  お疲れさまでした (写真は京都御苑) |
※ 3 桁の正の整数とは 100 から 999 までの整数をいう. ○ 3 で割り切れる数の集合を A で,5 で割り切れる数の集合を B で,7 で割り切れる数の集合を C で表わすとき,少なくとも1つで割り切れる個数は n(A∪B∪C) =n(A)+n(B)+n(C) - n(A∩B) - n(B∩C) - n(C∩A) +n(A∩B∩C) で求められる.  99÷5=19 … 4,999÷5=199 … 4 → n(B)=180 99÷7=14 … 1,999÷7=142 … 4 → n(C)=128 99÷15=6 … 9,999÷15=66 … 9 → n(A∩B)=60 99÷35=2 … 29,999÷35=28 … 20 → n(B∩C)=26 99÷21=4 … 15,999÷21=47 … 12 → n(C∩A)=43 99÷105=0 … 99,999÷105=9 … 4 → n(A∩B∩C)=9 300+180+128 - 60 - 26 - 43+9=488 100 から 999 までには 900 個の整数があるから 900 - 488=412 |