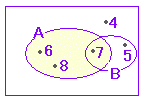
| (1) 70 人の学生について通学手段を調査したところ,電車を利用する学生は 24 人,バスを利用する学生は 27 人,自転車を利用する学生は 32 人,電車もバスも利用する学生は 7 人,バスも自転車も利用する学生は 11 人,自転車も電車も利用する学生は 9 人,3種類とも利用する学生は 3 人で,他は徒歩だけで通学していた. 徒歩だけで通学している学生は何人か. 
|
(1) ※ この文脈で「電車を利用する」とは,「電車だけを利用する」という意味ではなく,「少なくとも電車を利用する(他の手段も利用する者も含まれる)」という意味に理解する.(そうでなければ電車,バス,自転車の利用者合計が70人を越えてしまう.) 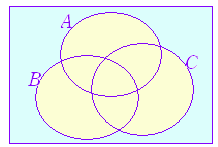 n(A∪B∪C) =n(A)+n(B)+n(C) - n(A∩B) - n(B∩C) - n(C∩A) +n(A∩B∩C) =24+27+32 - 7 - 11 - 9+3=59 ○ 求めるのは,水色で示した部分の人数 (全体の人数) - n(A∪B∪C) =70 - 59=11 ※ この基本公式は,すぐ使えるようにしておくとよい.公式に代入すれば直ちに解答にたどり着く問題も少なくない. |
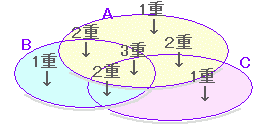
| (2) 50 人の学生が食堂でトーストを食べたとき,トーストに何をつけたか尋ねたところ,バターをつけた学生は 18 人,ハチミツをつけた学生は 27 人,ジャムをつけた学生は 25 人,バターもハチミツもつけた学生は 6 人,ハチミツもジャムもつけた学生は 12 人,ジャムもバターもつけた学生は 7 人,3種類ともつけた学生は 2 人であった. バターだけをつけた学生は何人か. |
(2) 公式だけでは分かりにくい問題は,ベン図を描いて考える.その際,分かっている部分には数値を書き込むとよい.この問題は次の図のように,単なる引き算で解決できる.(この問題では使用しない数字が幾つかある.) 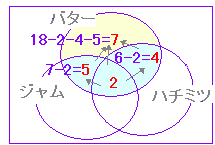
|
| (3) 200 以下の正の整数で 6 , 7 , 8 のいずれでも割り切れないものは何個あるか.  |
(3) ○ (1)の問題と同様にして,6 で割り切れる数の集合を A で,7 で割り切れる数の集合を B で,8 で割り切れる数の集合を C で表わすとき,少なくとも1つで割り切れる個数は n(A∪B∪C) =n(A)+n(B)+n(C) - n(A∩B) - n(B∩C) - n(C∩A) +n(A∩B∩C) で求められ いずれでも割り切れない個数は (全体の個数 200) - n(A∪B∪C) で求められる. ○ 例えば 6 で割り切れる数,すなわち 6 の倍数は 200÷7=28 ··· 4 から求められる. ○ 6 と 7 の両方で割り切れる数,すなわち 42 の倍数は 200÷42=4 ··· 32 から求められる.→ n(A∩B)=4 同様にして 200÷56=3 ··· 32 から→ n(B∩C)=3 200÷24=8 ··· 8 から→ n(C∩A)=8 ○ 6 7 , 8 のいずれでも割り切れる数,すなわち 168 の倍数は 200÷168=1 ··· 32 から→ n(A∩B∩C)=1 ○ 以上から n(A∪B∪C) =n(A)+n(B)+n(C) - n(A∩B) - n(B∩C) - n(C∩A) +n(A∩B∩C)=33+28+25 - 4 - 3 - 8+1=72 (全体の個数 200) - n(A∪B∪C)=200 - 72=128 |
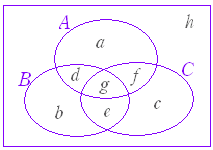
| (4) 3 桁の正の整数で 3 , 4 , 5 のうち2つ以上で割り切れるものは何個あるか. 
|
※ 3 桁の正の整数とは 100 から 999 までの整数をいう. ※ 1から始まっているのではなく,100以上で各々最初に当てはまる数がずれているので,割り算だけでは倍数の個数は求まらない.そこで,1〜999の範囲で該当するものから1〜99までの範囲で該当するものを引けば100〜999までの範囲で該当するものが求まる. ○ ベン図を描いて次のように数字を埋めていくとよい. 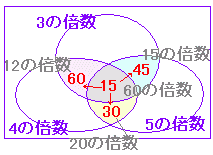 (75+45+60 - 15 ではないので注意.60 の倍数を2回数えてはいけない.) |