筆算固有の問題

== 筆算だけで解く問題 == ■　筆算だけで解くとは

　自宅や学校で学習しているときは，教科書の巻末についている三角関数表を見ることもできますし，あればコンピュータも利用することができます．だから，普通の状況では，sin46°とかcos12°のような覚えていない角度の三角比の値でも自由に使える（ただし小数点以下第４位までの小数の値）ことになっています．
　これに対して数学の試験の場合には，特に許可されない限り数表やコンピュータ，携帯電話は持ち込めないのが普通です．このように，高校生が最もよくであう場面では，問題は「筆算だけ」で解かなければなりません．
　このように数学の試験のように「筆算だけで解かなければならない問題」ではsin75°，cos105°のような値は，覚えていないから使えないことになります．

　そこで，sin75°，cos105°などの値が必要になったら，別の角度を利用する方法を探します.
　このときに用いられるものには，「正弦定理」「余弦定理」の他，余弦定理で２次方程式を作る方法，第一余弦定理，三角形の内角の和があります.

余弦定理で(ａの)２次方程式を作る：

ｂ²＝ｃ²＋ａ²－２ｃａ・ｃｏｓＢ　など

［第一余弦定理］
(解説）
次の図のように，Ａから垂線をひくと，
a=b・cosC+c・cosB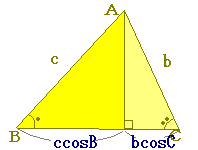

　この関係はＢ≧90°またはＣ≧90°の場合にも成立します.
　第一余弦定理は，1つの辺(ａ)の大きさを求めるために，辺の長さ２個，角の大きさ２個を必要とするため，余弦定理よりも「弱い」定理ですが，角Ａの値が利用できないような場合に有効です.
　この関係を第一余弦定理，(通常用いる)余弦定理のことを第二余弦定理と呼ぶことがあります.

例
　ａ＝2，Ａ＝45°，Ｃ＝75°のとき辺ｃの長さを求めなさい.

(第一印象)
　正弦定理a/sinA=c/sinC　を利用すればｃが求められるように思えますが，sin75°の値が使えません.
(答案)
三角形の内角の和は180°だから，Ｂ＝60°
正弦定理により，a/sinA=b/sinB　だから，ｂ＝asinB/sinA=√6

第一余弦定理により，ｃ＝ａｃｏｓＢ＋ｂｃｏｓＡ＝2・1/2＋√6・1/√2=1+√3・・・(答)

参考：
(別解1)　Ａ＝45°，ａ＝2 , ｂ＝√6から角Ａを用いた余弦定理から２次方程式を作ると，
　a²=b²+c²-2bc・cosA
　4＝6＋c²-2√6ｃ・1/√2
　c²-2√3ｃ+2＝0
　解の公式から　ｃ＝√3±1・・・（このままでは，いずれが答か，両方とも答なのか決まりません.）
　Ｃ＞Ａによりｃ＞ａとなるからｃ＝√3+1・・・(答)

(別解2)　Ｂ＝60°，ｂ＝√6から角Ｂを用いた余弦定理から２次方程式を作ると，
　ｂ²＝ｃ²＋ａ²－２ｃａ・ｃｏｓＢ
　6＝ｃ²+4-2ｃ・2・1/2
　ｃ²-2ｃ-2＝0
　解の公式から　ｃ＝1±√3，　ｃ＞0によりｃ＝1＋√3・・・(答)

※(第二)余弦定理で２次方程式を作る方法は，有力な方法です.この方法を用いるときには，見かけの解が２つ登場する場合がありますので，上の例のように吟味して答を選びます.

《問題》　次の△ＡＢＣについて指定されたものを下の選択肢から選びなさい．

(1)　$\displaystyle a=2\sqrt{2},b=2,B=30^{\circ}$のとき，$c$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

余弦定理b2=c2+a2−2ca cos Bに代入
$4=c^2+ 8-2c\times 2\sqrt{2} \times \frac{\sqrt{3}}{2}$
$c^2-2\sqrt{6}c+4=0$
解の公式を使って解くと
$c=\sqrt{6}\pm \sqrt{2}$
→閉じる←

(2)　$\displaystyle b=2\sqrt{2},c=2\sqrt{3},C=60^{\circ}$のとき，$a$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

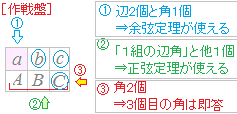辺が２つ分かっているから，右の作戦盤①で解く．
余弦定理
c2=a2+b2−2ab cos Cに代入
$12=a^2+ 8-2a\times 2\sqrt{2} \times \frac{1}{2}$
$a^2-2\sqrt{2}a-4=0$
解の公式を使って解くと
$a=\sqrt{2}\pm \sqrt{6}$
a>0だから
$a=\sqrt{2}+ \sqrt{6}$
（参考）
右の作戦盤②により角Ｂを求めてから，次に③により角Ａを求め，さらに②により辺aを求める作戦はＡが75°になるので筆算では行き詰ります．
右の作戦盤②により角Ｂを求めると辺角2組がそろうので，次に第1余弦定理により辺aを求めることはできます．
≪この場合の答案の流れ≫
正弦定理によりB=45°(Ｂ=135°はＣ=60°と矛盾)
第1余弦定理により $a=b\cos C+ c\cos B=\sqrt{2}+ \sqrt{6}$ →閉じる←

(3)　$\displaystyle a=3+\sqrt{3},b=2\sqrt{3},B=45^{\circ}$のとき，$c$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

辺が２つ分かっているので， cos Bを含む余弦定理
b2=c2+a2−2ca cos Bに代入
$12=c^2+ (3+ \sqrt{3})^2-2c(3+ \sqrt{3})\times \frac{1}{\sqrt{2}}$

ハードルが
高いジャン！

$c^2-\sqrt{2}(3+ \sqrt{3})c+ 6\sqrt{3}=0$
$(c-3\sqrt{2})(c-\sqrt{3}\sqrt{2})=0$
$c=3\sqrt{2},\sqrt{6}$
→閉じる←

(4)　$\displaystyle a=\sqrt{2},B=105^{\circ},C=45^{\circ}$のとき，$c$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

三角形の内角の総和は180°だから
A=180°−(B+C)=30°
A=30°,C=45°を使って正弦定理により解くと
$\frac{a}{\sin A}=\frac{c}{\sin C}$
$c=\frac{a\sin C}{\sin A}=\frac{\sqrt{2}\times \frac{1}{\sqrt{2}}}{\frac{1}{2}}=\sqrt{2}\times \frac{1}{\sqrt{2}}\times \frac{2}{1}=2$
→閉じる←

(5)　$\displaystyle a=\sqrt{6},A=30^{\circ},B=15^{\circ}$のとき，$c$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

三角形の内角の総和は180°だから
C=180°−(A+B)=135°
A=30°,C=135°を使って正弦定理により解くと
$\frac{a}{\sin A}=\frac{c}{\sin C}$
$c=\frac{a\sin C}{\sin A}=\frac{\sqrt{6}\times \frac{1}{\sqrt{2}}}{\frac{1}{2}}=\sqrt{6}\times \frac{1}{\sqrt{2}}\times \frac{2}{1}=2\sqrt{3}$
→閉じる←

(6)　$\displaystyle a=2\sqrt{3},b=2\sqrt{2},A=120^{\circ}$のとき，$c$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

辺が２つ分かっているので， cos Aを含む余弦定理
a2=b2+c2−2bc cos Aに代入
$12=8+ c^2-2\times 2\sqrt{2}\times c(-\frac{1}{2}})$
$c^2+2\sqrt{2}c-4=0$
解の公式により
$c=-\sqrt{2}\pm\sqrt{6}$
$c\gt 0$ により $c=-\sqrt{2}+\sqrt{6}$
→閉じる←

(7)　$\displaystyle b=2,A=15^{\circ},B=135^{\circ}$のとき，$c$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

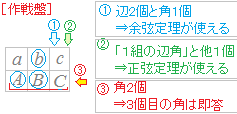右の作戦盤③で，三角形の内角の総和は180°だから
C=180°−(A+B)=30°
B=135°,C=30°を使って正弦定理により解くと
$\frac{b}{\sin B}=\frac{c}{\sin C}$
$c=\frac{b\sin C}{\sin B}=\frac{2\times \frac{1}{2}}{\frac{1}{\sqrt{2}}}=2\times \frac{1}{2}\times \frac{\sqrt{2}}{1}=\sqrt{2}$
→閉じる←

(8)　$\displaystyle c=2,A=15^{\circ},B=120^{\circ}$のとき，$a$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

三角形の内角の総和は180°だから
C=180°−(A+B)=45°
B=120°,C=45°を使って正弦定理により解くと
$\frac{b}{\sin B}=\frac{c}{\sin C}$
$b=\frac{c\sin B}{\sin C}=\frac{2\times \frac{\sqrt{3}}{2}}{\frac{1}{\sqrt{2}}}=2\times \frac{\sqrt{3}}{2}\times \frac{\sqrt{2}}{1}=\sqrt{6}$
２辺が分かったので余弦定理と使うと
$b^2=c^2+ a^2-2ca\cos B$
$6=4+ a^2-2\times 2a\times (-\frac{1}{2})$
$a^2+ 2a-2=0$
$a=-1\pm \sqrt{3}$
$a\gt 0$ により $a=-1+ \sqrt{3}$
→閉じる←

(9)　$\displaystyle a=3\sqrt{2},c=2\sqrt{3},A=60^{\circ}$のとき，$b$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

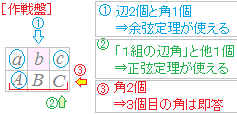辺が２つ分かっているから，右の作戦盤①で解く．
余弦定理
a2=b2+c2−2bc cos Aに代入
$18=b^2+ 12-2b\times 2\sqrt{3} \times \frac{1}{2}$
$b^2-2\sqrt{3}b-6=0$
解の公式を使って解くと
$b=\sqrt{3}\pm 3$
b>0だから
$b=\sqrt{3}+ 3$
（参考）
右の作戦盤②により角Ｃを求めてから，次に③により角Ｂを求め，さらに②により辺bを求める作戦はＢが75°になるので筆算では行き詰ります．
右の作戦盤②により角Ｃを求めると辺角2組がそろうので，次に第1余弦定理により辺ｂを求めることはできます．
≪この場合の答案の流れ≫
正弦定理によりC=45°
第1余弦定理により $b=a\cos C+ c\cos A=\sqrt{3}+ 3$ →閉じる←

(10)　$\displaystyle b=2,B=30^{\circ},C=105^{\circ}$のとき，$a$を求めなさい．

$\sqrt{2}$ $2$ $2\sqrt{2}$
$ 2\sqrt{3}$ $\sqrt{3}-1 $ $3+\sqrt{3}$
$\sqrt{6}-\sqrt{2}$ $\sqrt{2}+\sqrt{6}$ $\sqrt{6}\pm\sqrt{2}$ $3\sqrt{2},\sqrt{6}$

解説やり直す

三角形の内角の総和は180°だから
A=180°−(B+C)=45°
A=45°,B=30°を使って正弦定理により解くと
$\frac{a}{\sin A}=\frac{b}{\sin B}$
$a=\frac{b\sin A}{\sin B}=\frac{2\times \frac{1}{\sqrt{2}}}{\frac{1}{2}}=2\times \frac{1}{\sqrt{2}}\times \frac{2}{1}=2\sqrt{2}$
→閉じる←

←メニューに戻る　　