三角不等式

== 三角不等式 ==

〇高校数学で三角不等式という用語は２つの場面で登場します．
(1)　絶対値記号や距離に関して成り立つ不等式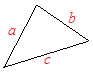

|x+y|≦|x|+|y|
もしくは，三角形の「２辺の長さの和」が「他の１辺の長さ」よりも大きいという関係式
c<a+b
（ベクトルで書くときは $\mid \vec{a}+ \vec{b}\mid \lt \mid \vec{a}\mid+ \mid \vec{b} \mid$ ）

(2)　三角関数で角度θの範囲を未知数とする不等式

$\sin \theta \gt \frac{1}{2}$ や $\sqrt{2}\sin \theta \gt -1$
$\cos \theta \lt -\frac{\sqrt{3}}{2}$ や $2\cos \theta + 1\lt 0$

(1)(2)のどちらの意味で使われているかは，前後の文脈を見れば分かるが，ここでは(2)の意味の「三角関数で角度θの範囲を求める」問題を扱う．

＃危険な落とし穴に注意＃
〇この項目を三角比のグラフで説明する立場もある．

〇しかし，例えば三角比のグラフ $y=2\cos \theta + 1$ が正確に書ければ，三角不等式 $2\cos \theta + 1\lt 0$ は解けるはずであるが，このグラフを正確に描こうとすると「ほとんどの生徒は時間がかかり過ぎ，テスト時間内に何個もできない．」
　もっと意地悪く $2\cos (3\theta-90^{\circ}) + 1\lt 0$ のような問題にすると，もう時間内にグラフが書ける生徒はほとんどいなくなる．

三角不等式の問題は「グラフを使わずに」「単位円」で解くとよい．

【例】
$2\cos \theta + 1\lt 0$ (0°≦θ≦180°)

$\cos \theta \lt -\frac{1}{2}$
に変形して，単位円の図を見ながら解くとよい．

右図により， $\cos \theta \lt -\frac{1}{2}$ となるθの値の範囲は
120°<θ≦180°
が答になる．

※単位円では180°が左に120°が右にあるように見えるので，180°≦θ<120°のような初歩的な間違い答案が多く見られる．
角度は不等号の向きに合わせて120°<θ≦180°のように書く．

《問題》　0°≦θ≦180°のとき，次の不等式を解きなさい． ○はじめに左の問題から一つクリックし，続けて右の答から１つをクリックしたとき，合っていれば消えます．間違いの場合は１秒後に元に戻ります． ○ヒントは下の方に出ます． ○左の問題を選択したら，右の答を選ばない限り次の問題には進めません．

(携帯版)...メニューに戻る

...（PC版）メニューに戻る